PA1 - FedUps

Package delivery isn’t what it used to be. With a rise in premium package delivery services, FedEx and UPS have now created a new tier in their delivery service options: FedUps sub-premium delivery subscription service. Subscribers to FedUps will receive a small discount on their shipping costs, but they must agree to receive only the worst customer treatment and delivery times for all packages. One example of this intentionally poor treatment is that FedUps will now send your packages to you via routes that are not guaranteed to be the most efficient. Instead, FedEx and UPS will try to use FedUps orders to do their best to minimize the excess capacity of all of their vehicles.

Requirements

Your algorithm will receive two weighted graphs (lists of edges) as input. The first graph will represent the transportation capacities of their vehicles. The nodes represent cities, edges represent trucks travelling between cities, and the weight of the edge represents the maximum weight that can be carried by each truck. The second graph will represent the current load on all vehicles. The same nodes and edges will be present as for the first graph, but now the edges represent the current weight of all cargo in each truck.

Your goal will be to write an algorithm which finds the path from a given start city to a destination city which minimizes the sum of load percentages (load/capacity) across all trucks used. Note that the number of trucks is irrelevant, we only care to minimize the sum of percentages. At-capacity trucks may not be used, since FedUps could not add a package to that truck.

Input

Your input will be 4 parameters containing the following information:

• numCitites - the number of total cities.
• capacities - a list of capacities of each of the trucks, given as a list of strings. Each string in the list contains a comma-separated list of integer values: the truck’s starting city, the truck’s destination city, and the truck’s carrying capacity.
• loads - a list of current loads of each of the trucks, given as a list of strings. Each string in the list contains a comma-separated list of integer values: the truck’s starting city, the truck’s destination city, and the truck’s current load.
• start - the start city.
• end - the destination city.

Output

Your output will be a list of integers indicating the sequence of cities which starts in the start city and ends in the destination city that also minimizes the cumulative sum of percentage of truck loads. The main method provided will print this list one city per line. An example output is given below.

Running Time Requirements

The worst-case asymptotic running time of your program should belong to \(O(c \cdot t)\), where \(c\) is the number of cities and \(t\) is the number of trucks.

Example

The graph below would be the result of the input given. In this case the path your algorithm should retun would be [0,2,3]. This path has cost 120 (because it is \(60\%+60\%\)). The path 0,1,3 would have cost 133.34 (\(66.67\%+66.67\%\)). The path 0,3 is not valid because the edge is already at capacity. After your program finishes, the following text should be printed to the console:

0
2
3

Example Visualized

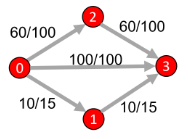
Example Input

• numCities = 4
• capacities the list:

    0,3,100
    0,1,15
    0,2,100
    1,3,15
    2,3,100
  

• loads the list:

    0,3,100
    0,1,10
    0,2,60
    1,3,10
    2,3,60
  

• start = 0
• end = 3

Submission Requirements

• Your algorithm must be written in Python 3.10.6 or Java 19.0.2 (OpenJDK)
• You must download the appropriate wrapper code based on the language you choose: Main.py, FedUps.py, and Graph.py for Python; Main.java, FedUps.java, and Graph.java for Java.
  • Java package: pa1-java.zip
  • Python package: pa1-python.zip
• Implement the compute() method in the FedUps class. The compute() method should execute the entirety of your algorithm and return the list of cities in the path.
• Implement the Graph class using an Adjacency List graph implementation. You should then use this in your FedUps class.
• You may modify the Main.java or main.py files to test your algorithm, but they will not be used during grading.
• You must submit your {FedUps.java and Graph.java} or {FedUps.py and Graph.py} files on Gradescope. Do not submit Main.java, main.py, or any test files.
• A few other notes:
  • Your code will be run as:
    python Main.py or python3 Main.py for Python,
    or javac *.java && java Main for Java.
  • You may upload multiple Java files if you need addional classes, but do not assign packages to the files.
  • You may not use any graph packages for this assignment.
  • Please note that you are responsible for analyzing the running time of any algorithm you use and ensuring that they satisfy the runtime requirements for this assignment.

Rules on Collaboration and Outside Sources

You must follow the rules about Collaboration and Outside Sources in the syllabus.

Use of Generative AI

For PA1, you are not allowed to use generative AI tools to help you solve this problem.