PDR: Laboratory 9: x86 Assembly Language, part 2 (64 bit)

Go up to the Labs table of contents page

Objective

This lab is one of two labs meant to familiarize you with the process of writing, assembling, and linking assembly language code. The purposes of the in-lab and in-lab activities are to investigate how various C++ language features are implemented at the assembly level.

There are both 32 bit (md) and 64 bit (md) versions of this lab. This is the 64 bit version.

Background

The Intel x86 assembly language is currently one of the most popular assembly languages and runs on many architectures from the x86 line through the Pentium 4. It is a CISC instruction set that has been extended multiple times (e.g. MMX) into a larger instruction set.

Tutorial

Read the C tutorial for the in-lab.

  1. Read the slides on x86
  2. The two book chapters on x86: x86 Assembly and The x86 C Calling Convention.
  3. The x86 Assembly Guide from an older course at UVA (ignore the section on Calling Convention)

Lab Procedure

Pre-lab

  1. Create an assembly program to demonstrate the Collatz conjecture
  2. Time your program using a helper C++ file
  3. Optimize your program and list all optimizations used
  4. Files to download: timer.cpp (src), timer.h (src) (from the lab 6 directory)
  5. Files to submit: threexplusone.s, threexinput.cpp, timer.cpp, timer.h, Makefile

In-lab

  1. Complete the provided linkedlist.c program by going through Tutorial 9: C (md)
  2. Files to download: linkedlist.c (src)
  3. Files to submit: linkedlist.c, Makefile

Post-lab

  1. Write an x86 function to perform a binary search
  2. Files to download: testBinarySearch.cpp (src), timer.cpp (src), and timer.h (timer.h)
  3. Files to submit: testBinarySearch.cpp, binarySearch.s, timer.cpp, timer.h, Makefile

Pre-lab

You may want to reference the “Compiling Assembly With C++” and “Vecsum” sections from the previous x86 lab.

The Collatz Conjecture

The 3x+1 conjecture (also called the Collatz conjecture) is an open problem in mathematics, meaning that it has not yet been proven to be true. The conjecture states that if you take any positive integer, you can repeatedly apply the following function to it:

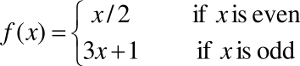
The conjecture is that eventually, the result will reach 1. For example, consider x = 13:

  1. f(13) = 3 * 13 + 1 = 40
  2. f(40) = 40 / 2 = 20
  3. f(20) = 20 / 2 = 10
  4. f(10) = 10 / 2 = 5
  5. f(5) = 3 * 5 + 1 = 16
  6. f(16) = 16 / 2 = 8
  7. f(8) = 8 / 2 = 4
  8. f(4) = 4 / 2 = 2
  9. f(2) = 2 / 2 = 1

Note that this took 9 steps to reach the value 1. And it also shows that this conjecture is true for a number of other values (2, 4, 5, 8, 10, 16, 20, and 40).

An image (from Wikipedia) shows how paths of most integers less than 50 converge to 1.

While this conjecture has been proven only up to at least 5.6 * 10^13, it is widely believed to be true for all positive integers. If you are interested, more information on this conjecture can be found here.

We won’t be testing with any values above 10^6, so you can safely assume that the Collatz conjecture holds true for all of the input values that we will use. That is, you won’t have to worry about integer overflow.

Your task is to write a routine, called threexplusone, that takes in a positive integer and returns the number of steps required for that integer to reach 1 by following the Collatz conjecture. An input of 13 takes 9 steps, as shown above. The Wikipedia page shows a few other input sizes and the number of steps: an input of 6 takes 8 steps; an input of 14 takes 17 steps; an input of 27 takes 111 steps. If the input is 1, the output should be zero.

This routine MUST call itself recursively using the proper C-style calling convention. The assembly code should be in a threexplusone.s file. If you write your function so that it is an iterative solution, you will not receive credit for this pre-lab.

Testing and timing

You will need to write a C++ file called threexinput.cpp that allows you to test your subroutine. This input file should:

  1. Ask for an input value, x, which is the positive integer to pass to the subroutine
  2. Ask for an input value, n, which is the number of times to call the subroutine
  3. Run the subroutine once and store the result
  4. Run the subroutine n times with the parameter x as the input
  5. Print out the number of iterations it took for the integer to converge to 1.

You can assume that both x and n are positive integers.

We can now time the subroutine to see how fast it runs. Download the timer code from the hash table lab (lab 6: timer.cpp (src) and timer.h (src)) and use it to guage the average time it took to run each subroutine call in step 4.

You should use an appropriate precision number to make sure you don’t report zero when you divide the total time by the number of runs. Your timer code should only include the loop of n times that calls the routine with x as the parameter. Nothing else (including the print statement) should be inside the timer code.

Optimization

Now that you can time your program, you will need to optimize it as much as possible. Any optimization is valid, as long as it computes the correct result, is still a recursive subroutine, and follows the C calling convention. The grade on this pre-lab will be based both on the correctness of the subroutine and the optimizations included.

What optimizations do you use?

You will need to include at least one optimization beyond just figuring out how to write your subroutine with fewer instructions. You should put the optimizations used as a comment in the beginning of your assembly file.

Note that we, too, can write the function in C++ and compile it with clang++ -O2 -S -mllvm --x86-asm-syntax=intel. And we will be looking at that assembly code when we grade the pre-lab. If you write your program this way, it constitutes an honor violation, so please hand-code the assembly yourself.

You must list, as comments in your assembly file, the optimizations that you used! Just a brief description of what optimizations you used is fine.

Sample Execution Run

Below is a sample execution run to show you the input and output format we are looking for.

Input

Enter a number: 100
Enter iterations of subroutine: 30

Output

Steps: 25

Different Architectures

See the last lab for details, but all code must be submitted to run under Linux, which is the platform that does the compilation on the submission system.

In-lab

Complete the C tutorial’s exercise program

Download the linkedlist.c (src) test harness, your task is to implement a simple doubly-linked list in C. Read the C tutorial to help familiarize yourself with the C language. This linked list is meant to be simple, and can be implemented however you’d like in linkedlist.c. We don’t really care how you implement the linked list, whether it be with structs, arrays, etc. so long as it works with the provided harness. However, the assignment is considerably easier to do by using an actual linked list solution rather than an array-based solution. Your linked list will need to be able to do the following:

Sample Execution Run

Below is a sample execution run to show you the input and output format we are looking for.

----------------------------------------------------
This test harness operates with one linked list.
Use any of the following options to manipulate it:
        * af <num> --- add integer to front
        * ab <num> --- add integer to back
        * rf       --- remove front element
        * rb       --- remove back element
        * p        --- print list forward
        * help     --- print off this list
        * -1       --- exit harness

Enter command: af 1
Enter command: af
Invalid command or operand, please input a valid command or help to see the list again.
Enter command: af 2
Enter command: ab 3
Enter command: p
Elements: 2 1 3
Enter command: rf
Enter command: p
Elements: 1 3
Enter command: rb
Enter command: p
Elements: 1
Enter command: -1

Post-Lab

Download testBinarySearch.cpp (src), timer.cpp (src), and timer.h (timer.h), which you will use to test your code. Make sure you do not alter any of these files, as your must include the original files in your submission.

Your task for the post-lab is to implement the binarySearch function in assembly. This function will begin at the middle of a sorted array, and continuously split the search space in half until it finds the target element or reaches a point where it knows the target is not in the array. The function takes in four parameters. The first parameter is a pointer to an int array. The second parameter is an integer representing the beginning of the array. The third parameter is an integer representing the end of the array. The fourth parameter is an integer representing the target element to find in the array. The return type of this function is int, and will be the index into the array that the target was found, or -1 if it wasn’t. Just like with the linearSearch from Post-Lab 8, testBinarySearch will take input from std and pass it on to your binarySearch routine. Make sure you test your function on various sized arrays.

To make sure your function is efficient enough, the testBinarySearch.cpp file will call your function 1000 times and record the overall time taken via timer.cpp.

Sample Execution Run

Below is a sample execution run to show you the input and output format we are looking for.

Enter the array size: 5
Enter value 0: -30
Enter value 1: -15
Enter value 2: 0
Enter value 3: 15
Enter value 4: 30
Enter target to search for: 30

Found 30 at index 4
Took 0.007ms

The following resource explains the binary search algorithm. This is what you need to implement in x86 assembly: https://www.hackerearth.com/practice/algorithms/searching/binary-search/tutorial/