PA1 - Marriage

It’s the day we’ve all been waiting for; Luke and Lorelai are finally getting married! Luke and Lorelai have both arrived at the chapel at the same time (at different entrances), and must get to their respective dressing rooms. American wedding tradition says that it is bad luck for the bride and groom to see each other on the day of their wedding before the ceremony. Lorelai’s daughter, Rory, needs your help as a DSA2 student, in finding the shortest paths for Luke and Lorelai to take ensuring that neither is in the other’s line-of-sight.

Requirements

The input you are given is a connected undirected graph, with each node representing a room in the chapel, and edges indicating that those rooms are adjacent. The following items outline the requirements and constraints.

• Luke and Lorelai can only travel between adjacent rooms.
• They are within the other’s line-of-sight if and only if they simultaneously occupy the same or adjacent rooms.
• Luke and Lorelai move at the same time, so you can think of their motion in terms of time steps where each one moves to an adjacent room or chooses to remain in their current room. Again, the restriction is that Luke and Lorelai can never occupy the same room or adjacent rooms at any single time step.
• We’ll refer to the sequence of rooms where a person is located at each time step as a “schedule.” Since both move together, the schedules you find for the bride and for the groom will be the same length. (See the example given below.)
• You may assume that there always exists at least one pair of schedules for Luke and Lorelai that satisfies these requirements.
• If there are more than one pair of valid schedules, return the pair of schedules that is the shortest (in terms of time steps).

Note: it’s clear that some kind of algorithm that finds a shortest path is needed, but the input graph you’re given models rooms and their connections. The path you need to find is made up of moves that Luke and Lorelai take at each time step.

Input

Your algorithm will receive as input the body (list of strings) of a file called chapel.txt. The first line of this file will contain an integer \(n\) representing the number of rooms (vertices) in the chapel (graph). We will refer to each vertex by an integer between \(0\) and \(n-1\); i.e., by an index. The next 2 lines will each contain two space-separated integers between \(0\) and \(n-1\). The first of the two lines indicates the start and end vertices for Luke, respectively. The second of those two lines indicates the start and end vertices for Lorelai, respectively. The remaining \(n\) lines will respectively (in order of index) list each vertex’s neighboring vertices as space-separated integers each between \(0\) and \(n-1\), collectively giving an adjacency list representation of the graph. An example input is given below.

chapel.txt

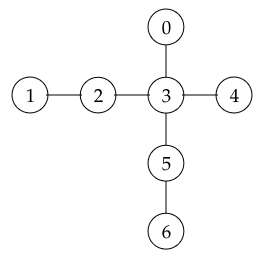
    7
    0 6
    2 4
    3
    2
    1 3
    0 2 4 5
    3
    3 6
    5

chapel visualized

Output

Your output will be the length of the shortest path that they must collectively take as well as providing the exact paths that each must take. The main method provided will first display the length of the path, then will give the schedule for Luke, and then the schedule for Lorelai. A schedule is the sequence of vertices each must take simultaneously so that they do not occupy the same or adjacent vertices at the same time. Because the shortest path may not be unique, you can return any valid shortest path that satisfies the requirements. An example output is given below.

    5
    [0, 3, 5, 6, 6]
    [2, 1, 2, 3, 4]

Study these results to see how Luke moves from room 0 to room 6 while Lorelai moves from room 2 to room 4 without violating the problem’s constraints.

Runtime requirements

Your algorithm must run in \(O(n^4)\) time, where \(n\) is the number of rooms in the chapel. (Note: for testing, your algorithm will be limited to at most 10GB of memory and a reasonable amount of compute time. However, you should not be reaching either of these limits with a \(O(n^4)\) runtime.)

Submission Requirements

• Your algorithm must be written in Python 3.10.6 or Java 19.0.2 (OpenJDK)
• You must download the appropriate wrapper code based on the language you choose: main.py and marriage.py for Python, Main.java and Marriage.java for Java.
  • Java package: pa1-java.zip
  • Python package: pa1-python.zip
• Implement the compute() method in the Marriage class. The compute() method should execute the entirety of your algorithm, return the length of the shortest path, and store the paths for Luke and Lorelai in the given class fields. We’ve provided getters for each of them.
• You may modify the Main.java or main.py files to test your algorithm, but they will not be used during grading.
• You must submit your Marriage.java or marriage.py files on Gradescope. Do not submit Main.java, main.py, or any test files.
• A few other notes:
  • Your code will be run as:
    python main.py or python3 main.py for Python,
    or javac *.java && java Main for Java.
  • You may upload multiple Java files if you need addional classes, but do not assign packages to the files.
  • You may not use any graph packages for this assignment.
  • Please note that you are responsible for analyzing the running time of any algorithm you use and ensuring that they satisfy the runtime requirements for this assignment.

Rules on Collaboration and Outside Sources

You must follow the rules about Collaboration and Outside Sources in the syllabus.

Use of Generative AI

For PA1, you are not allowed to use generative AI tools to help you solve this problem.