CS 2150 Roadmap
Data Representation | Program Representation | |||||
| string int x[3] char x 0x9cd0f0ad 01101011 |
 |
Objects Arrays Primitive types Addresses bits |
Java code C++ code C code x86 code IBCM hexadecimal |
 |
High-level language Low-level language Assembly language Machine code |
|
C++ Implementation of Arrays
- Array names are pointers to beginning of array
int someInts[3];- The size is only used by compiler to set aside memory for the array; it is not stored anywhere
someIntsis set to&someInts[0]- Also called the base address
- Local constant that cannot be changed
- Note that the previous declaration is almost the same as:
int* someInts = new int[3];- But since this second declaration is declared with
new, the programmer must delete it:delete []
- But since this second declaration is declared with
int someInts[3] = {2, 4, 6};
| Array part | Address | Memory |
|---|---|---|
&someInts[0] | 1000 | 2 |
&someInts[1] | 1004 | 4 |
&someInts[2] | 1008 | 6 |
| ... | ||
someInts | ??? | 1000 |
| ... |
This assumes that ints are 4 bytes in size
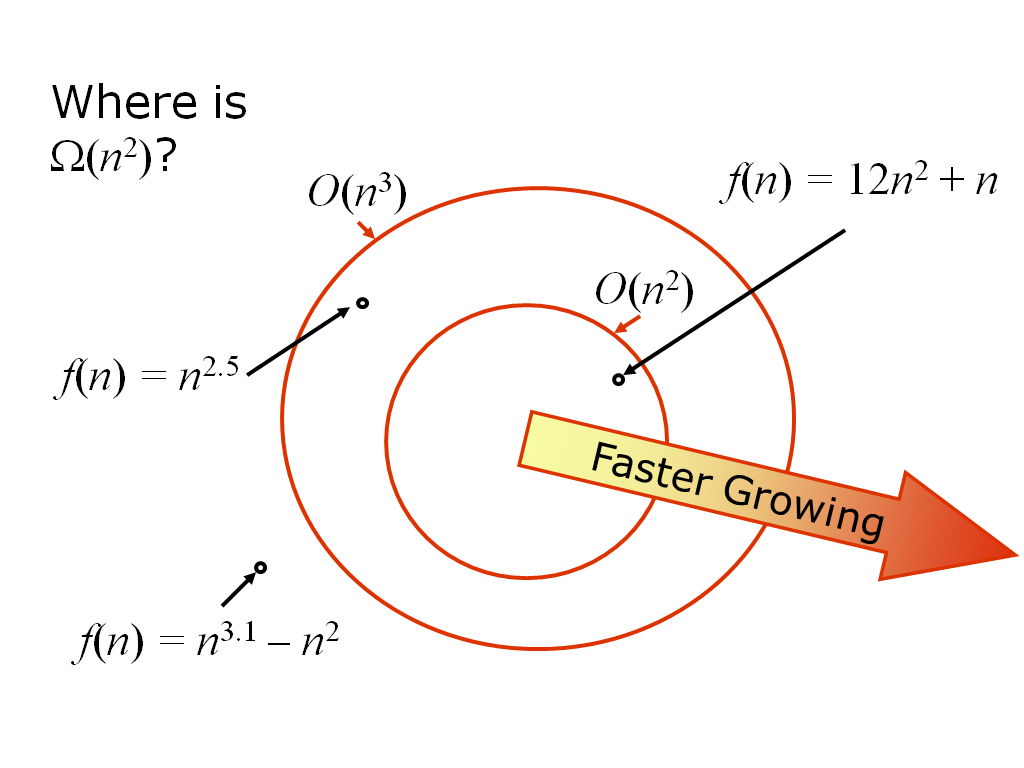
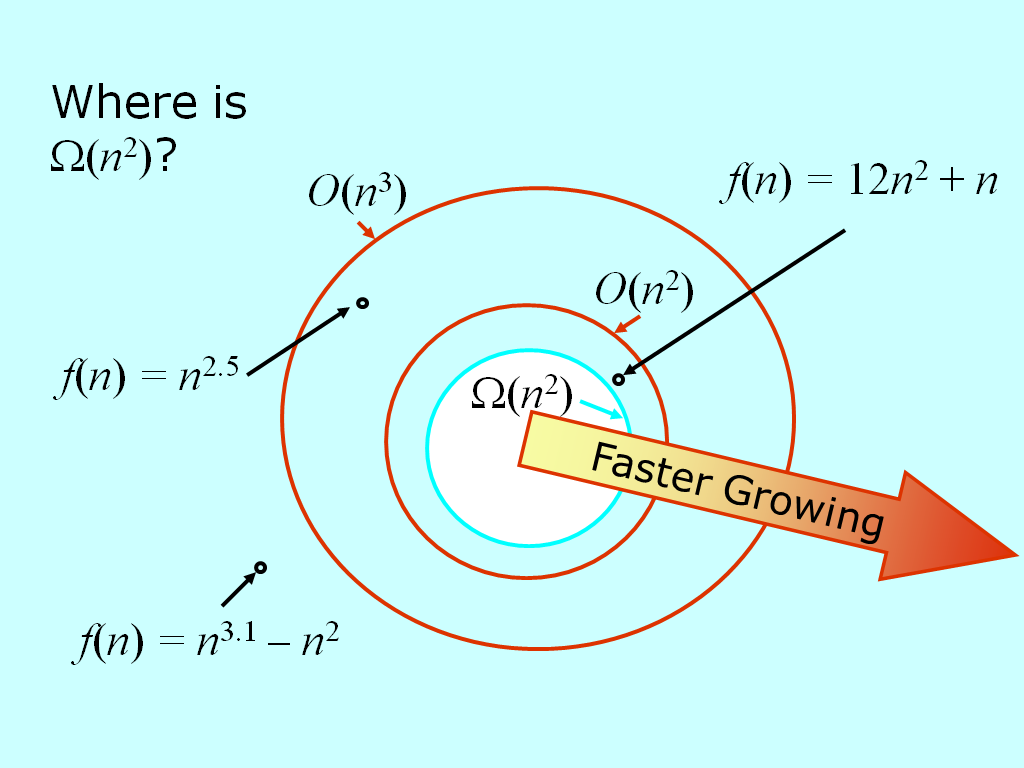
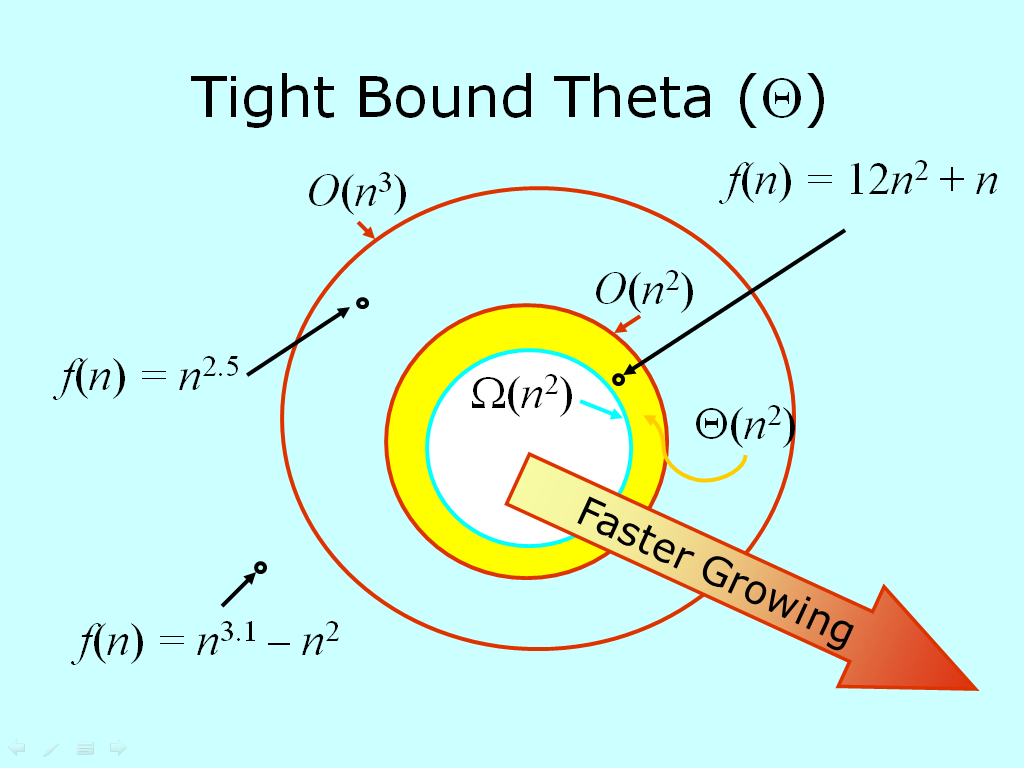
The Sets O(g), Θ(g), Ω(g)
- Let f and g be a functions from the non-negative integers into the positive real numbers
- For some real constant c > 0 and some non-negative integer constant n0
- O(g) is the set of functions f, such that:
- f(n) ≤ c * g(n) for all n ≥ n0
- Ω(g) is the set of functions f, such that:
- f(n) ≥ c * g(n) for all n ≥ n0
- Θ(g) = O(g) ∩ Ω(g)
- Θ(g) is the asymptotic order of g or the order of g
- f ∈ Θ(g) read as "f is asymptotic order g" or "f is order g"
- O(g) is the set of functions f, such that:
Big-Oh Examples
f(n) ∈ O(g(n)) means that there are positive constants c and n0 such that f(n) ≤ c*g(n) for all values n ≥ n0
- Is n ∈ O(n2)?
- Yes, c = 1, n0 = 2 works fine
- Is 10n ∈ O(n)?
- Yes, c = 11, n0 = 2 works fine
- Is n2 ∈ O(n)?
- No; no matter what values for c and n0 we pick, n2 > c*n for big enough n
Given f ∈ O(h) and g ∉ O(h),
which of these are true?
- For all positive integers m, f(m) < g(m).
- For some positive integer m, f(m) < g(m).
- For some positive integer m0, and all positive integers m > m0, f(m) < g(m).
- 1 and 2
- 2 and 3
- 1 and 3
Another Way to Define Order Classes
- Comparing f(n) and g(n) as n approaches infinity...
- If \( \lim{n \to \infty}\frac{f(n)}{g(n)} \) is:
- < ∞, including the case in which the limit is 0, then f ∈ O(g)
- > 0, including the case in which the limit is ∞, then f ∈ Ω(g)
- = c and 0 < c < ∞ then f ∈ Θ(g)
- = 0 then f ∈ o(g)
- read as "little-oh of g"
- = ∞ then f ∈ ω(g)
- read as "little-omega of g"