Go up to the Labs table of contents page
A binary tree is a tree with a maximum of two children per node. Tree traversals are commonly associated with binary trees. A pre-order traversal processes the given node first and then processes its left and then right subtrees. In an in-order traversal, first the node’s left subtree is processed, followed by the node itself, and finally its right subtree. A post-order traversal operates on the left subtree, followed by the right subtree, and finally on the node itself.
A binary search tree is a binary tree that imposes an ordering on its nodes. A node’s left child has a lesser value, while its right child has a greater value. Binary search trees are useful for efficient insertion, deletion, and lookup of items with a certain key. As we’ll see in this lab, variations of binary search trees offer different performance characteristics.
Complete the Makefile tutorial. You will need to know how to write one for the pre-lab, in-lab and post-lab, since all the following labs will be compiled via Makefiles.
The Wikipedia article on Expression trees, especially the section on construction of expression trees. Also the 05: Trees slide set.
For the pre-lab you will be using a stack to help you read in a postfix expression into an expression tree. While this is similar to lab 3, you will instead be ultimately creating an expression tree for the postfix expression, rather than evaluating it and leaving the result on the stack.
Your tree calculator will read in well-formed expressions in postfix notation. You will need to build an expression tree using the algorithm described in the Wikipedia article on Expression trees and the trees slide set. Trees similar to this type of expression tree are used extensively in compilers.
Your fully functional tree calculator must:
+: addition-: subtraction*: multiplication/: integer divisionAdditionally, you should use the skeleton source files in the prelab/
directory of code.zip as a basis for your tree
calculator. You may modify and add to the skeleton code as you see fit,
but TreeCalcTest, TreeNode, readInput(), and
printOutput() must NOT be modified.
Below is a sample execution run to show you the input and output format we are looking for.
Enter elements one by one in postfix notation
Any non-numeric or non-operator character, e.g. #, will terminate input
Enter first element: 34
Enter next element: 6
Enter next element: +
Enter next element: -8
Enter next element: 4
Enter next element: /
Enter next element: -
Enter next element: #
Expression tree in postfix expression: 34 6 + -8 4 / -
Expression tree in infix expression: ((34 + 6) - (-8 / 4))
Expression tree in prefix expression: - + 34 6 / -8 4
The result of the expression tree is 42You should submit any files required for your tree calculator to run. TreeCalcTest.cpp, TreeNode.h, and TreeNode.cpp should not be modified.
Recursion is the way to go: Recursion is very useful in traversing the expression tree. You’ll need to use recursion for many of the TreeCalc methods.
Printing in the right order: Draw a simple tree and see how you should recurse in order to hit each node in the correct order. Need more help? Check the Wikipedia article!
For this in-lab, you will implement a binary search tree.
The necessary files are in the inlab/ directory of code.zip.
The required class declarations are located in BinaryNode.h (src) and BinarySearchTree.h (src). You may want to create
private helper methods for BinarySearchTree, as done for the
implementation of remove(), which is already provided for
you. The private methods take BinaryNodes as parameters which allow them
to recurse over a subtree, a common implementation technique.
You should use BSTPathTest.cpp (src) to test your implementation, but you may NOT change it.
Unlike the pre-lab, you can modify the various files provided EXCEPT for BSTPathTest.cpp and AVLPathTest.cpp.
We provide a number of test files that you can use as input: testfile1.txt (output), testfile2.txt (output), and testfile3.txt (output)
The test program reads a sequence of instruction/word pairs and attempts to operate on your tree.
I <word>R <word>L <word>The Lookup instruction will call the pathTo() method
defined on your tree. pathTo() must return a string
representing the nodes encountered when finding an element. For instance
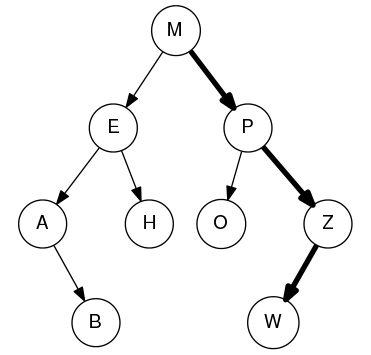
in the following image, the bold lines indicate the path taken for
locating element W.

pathTo("W") would then return the string "M P Z
W". Calling pathTo() on an element that doesn’t
exist would result in an empty string "".
Below is a sample execution run to show you the input and output format we are looking for.
I We
I can't
I solve
I problems
I by
I using
I the
I same
I kind
I of
I thinking
I we
I used
I when
I we
I created
I them
I -Albert
I Einstein
L created
BST path: We can't solve problems kind created
BST numNodes: 18You should submit your BST, any supporting C++ files, as well as a
Makefile to compile everything into an a.out
executable.
Private methods: Following the suggestion to implement private versions of all the public methods that take in BinaryNodes will help considerably. How should your public method interact with the private version? In other words, what node should the public method pass in?
Passing pointers by reference: When a pointer is passed by reference, that allows us to change not only the data that the pointer is pointing to, but also what the pointer is pointing to in the first place. This is one option that allows you to change the structure of your tree without having to use parent pointers.
The objective of this post-lab is to understand the run-time characteristics and trade-offs between normal Binary search trees and AVL trees. Your deliverable for this post-lab will be an AVL tree implementation.
The structure of the provided AVL starter code is analogous to that of the BST, and is not discussed in further detail here. The starter files are in the postlab/ directory of code.zip. The comments in the code of the starter files help explain where to start.
You may test your implementation with the same test files as before, though the expected output will be different (output of testfile1, output of testfile2, output of testfile3).
Unlike the pre-lab, you can modify the various files provided EXCEPT for BSTPathTest.cpp and AVLPathTest.cpp.
Below is a sample execution run to show you the input and output format we are looking for.
I We
I can't
I solve
I problems
I by
I using
I the
I same
I kind
I of
I thinking
I we
I used
I when
I we
I created
I them
I -Albert
I Einstein
L created
AVL path: problems can't kind created
AVL numNodes: 18You should submit your AVL tree, any supporting C++ files, and the Makefile.
balance(AVLNode*& node) is crucial for both insert
and remove, but has many cases that you must account for. To help avoid
potential issues, here is some pseudocode for the balance method that
you may use:
//Note that balance factor here is assumed to be (height of right subtree - height of left subtree)
balance(node):
if balance factor of node is 2 we will need to rotate left:
first, see if we should also rotate right (i.e., do a double rotation)
if balance factor of right child is negative:
rotate right on the right child
endif
rotate left on node
else if balance factor of node is -2 we will need to rotate right:
first, see if we should also rotate left (i.e., double rotation)
if balance factor of left is positive:
rotate left on the left child
endif
rotate right on node
endif