CS 3100

Data Structures and Algorithms 2

Dynamic Programming

Aaron Bloomfield (aaron@virginia.edu)
Raymond Pettit (raymond.pettit@virginia.edu)
@github | ↑ |

Introduction

Readings in CLRS 4th edition: chapter 14

Warm Up

\(2 \times n\) board with dominoes?

How many ways to tile this:

With these?

For example:

Warm Up

How many ways are there to tile a \(2 \times n\) board with dominoes?

Two ways to fill the final column:

\(n-1\)

\(n-2\)

\[Tile(0) = 1\] \[Tile(1) = 1\] \[Tile(n) = Tile(n-1) + Tile(n-2)\]

How to compute \(Tile(n)\)?

Tile(n):
    if n < 2:
        return 1
    return Tile(n-1) + Tile(n-2)

Problem?

Recursion Tree

Many redundant calls!	Run time: \(\Theta(1.6^n)\)
Better way: Use Memory!

Computing \(Tile(n)\) with memory

Initialize memory M
Tile(n):
    if n < 2:
        return 1
    if M[n] is filled:
        return M[n]
    M[n] = Tile(n-1)+Tile(n-2)
    return M[n]

Technique: memoization (note no ‘r’)

M
	0
	1
	2
	3
	4
	5
	6

Computing \(Tile(n)\) with memory

Initialize memory M
Tile(n):
    if n < 2:
        return 1
    if M[n] is filled:
        return M[n]
    M[n] = Tile(n-1)+Tile(n-2)
    return M[n]

M
1	0
1	1
2	2
3	3
5	4
8	5
13	6

Dynamic Programming

Requires Optimal Substructure
- Solution to larger problem contains the (optimal) solutions to smaller ones
Idea:
1. Identify recursive structure of the problem
  - What is the “last thing” done?

\(n-1\)

\(n-2\)

Dynamic Programming

Requires Optimal Substructure
- Solution to larger problem contains the (optimal) solutions to smaller ones
Idea:
1. Identify recursive structure of the problem
  - What is the “last thing” done?
2. Save the solution to each subproblem in memory

Generic Divide and Conquer Solution

def myDCalgo(problem):
- if baseCase(problem):
  - solution = solve(problem)
  - return solution
- for subproblem of problem: # After dividing
  - subsolutions.append(myDCalgo(subproblem))
- solution = Combine(subsolutions)
- return solution

Generic Top-Down DP Solution

def myDCalgo(problem):
- if baseCase(problem):
  - solution = solve(problem)
  - return solution
- for subproblem of problem:
  - subsolutions.append(myDPalgo(subproblem))
- solution = OptimalSubstructure(subsolutions)
- return solution

Generic Top-Down DP Solution

mem = {}
def myDCalgo(problem):
- if mem[problem] not blank:
  - return mem[problem]
- if baseCase(problem):
  - solution = solve(problem)
  - mem[problem] = solution
  - return solution
- for subproblem of problem: # After dividing
  - subsolutions.append(myDPalgo(subproblem))
- solution = OptimalSubstructure(subsolutions)
- mem[problem] = solution
- return solution

Computing \(Tile(n)\) with memory “Top Down”

Initialize memory M
Tile(n):
    if n < 2:
        return 1
    if M[n] is filled:
        return M[n]
    M[n] = Tile(n-1)+Tile(n-2)
    return M[n]

Recursive calls happen in a predictable order

M
1	0
1	1
2	2
3	3
5	4
8	5
13	6

Computing \(Tile(n)\) with memory “Bottom Up”

Tile(n):
    Initialize memory M
    M[0] = 1
    M[1] = 1
    for i = 2 to n:
      M[i] = M[i-1] + M[i-2]
    return M[n]

M
	0
	1
	2
	3
	4
	5
	6

Dynamic Programming

Requires Optimal Substructure
- Solution to larger problem contains the (optimal) solutions to smaller ones
Idea:
1. Identify recursive structure of the problem
  - What is the “last thing” done?
2. Save the solution to each subproblem in memory
3. Select a good order for solving subproblems
  - “Top Down”: Solve each recursively
  - “Bottom Up”: Iteratively solve smallest to largest

Log Cutting

Readings in CLRS 4th edition: chapter 14, specifically 14.1

Log Cutting

Find the best way to cut the log, given a log of length \(n\) and
a list (of length \(n\)) of prices \(P\) where \(P[i]\) is the price of a cut of size \(i\)

Price:	1	5	8	9	10	17	17	20	24	30
Length:	1	2	3	4	5	6	7	8	9	10

Select a list of lengths \(\ell_1, \ldots, \ell_k\) such that:
- \(\sum\ell_i=n\) to maximize \(\sum\color{blue}{P[\ell_i]}\)

Brute force: \(O(2^n)\)

Greedy Algorithm

Greedy algorithms build a solution by picking the best option “right now”

Select the most profitable cut first

Price:	1	18	24	36	50	50
Length:	1	2	3	4	5	6

Greedy: Lengths: 5, 1

Profit: 51

Better: Lengths: 2, 4

Profit: 54

Greedy Algorithm

Greedy algorithms build a solution by picking the best option “right now”

Select the “most bang for your buck”
- (best price / length ratio)

Price:	1	18	24	36	50	50
Length:	1	2	3	4	5	6

Greedy: Lengths: 5, 1

Profit: 51

Better: Lengths: 2, 4

Profit: 54

Dynamic Programming

Requires Optimal Substructure
- Solution to larger problem contains the (optimal) solutions to smaller ones
Idea:
1. Identify recursive structure of the problem
  - What is the “last thing” done?
2. Save the solution to each subproblem in memory
3. Select a good order for solving subproblems
  - “Top Down”: Solve each recursively
  - “Bottom Up”: Iteratively solve smallest to largest

1. Identify Recursive Substructure

\(P[i] =\) value of a cut of length \(i\)

\(Cut(n)=\) value of best way to cut a log of length \(n\)

\[{\color{magenta}Cut(n)} = \max \begin{cases} {\color{magenta}Cut(n-1)} + \color{blue}{P[1]} \\ {\color{magenta}Cut(n-2)} + \color{blue}{P[2]} \\ \color{black}{\ldots} \\ {\color{magenta}Cut(0)} + \color{blue}{P[n]} \end{cases}\]

\(Cut(n-\ell_k)\)

\(\ell_k\)

best way to cut a log of length \(n-\ell_k\)

last cut

Dynamic Programming

Requires Optimal Substructure
- Solution to larger problem contains the (optimal) solutions to smaller ones
Idea:
1. Identify recursive structure of the problem
  - What is the “last thing” done?
2. Save the solution to each subproblem in memory
3. Select a good order for solving subproblems
  - “Top Down”: Solve each recursively
  - “Bottom Up”: Iteratively solve smallest to largest

3. Select a Good Order for Solving Subproblems

Solve Smallest subproblem first

\[{\color{magenta}Cut(0)}=0\]

Cut(i):	0
Length:	0	1	2	3	4	5	6	7	8	9	10

3. Select a Good Order for Solving Subproblems

Solve Smallest subproblem first

\[{\color{magenta}Cut(1)}={\color{magenta}Cut(0)}+\color{blue}{P[1]}\]

Cut(i):	0
Length:	0	1	2	3	4	5	6	7	8	9	10

3. Select a Good Order for Solving Subproblems

Solve Smallest subproblem first

\[{\color{magenta}Cut(2)} = \max \begin{cases} {\color{magenta}Cut(1)} + \color{blue}{P[1]} \\ {\color{magenta}Cut(0)} + \color{blue}{P[2]} \\ \end{cases}\]

Cut(i):	0
Length:	0	1	2	3	4	5	6	7	8	9	10

3. Select a Good Order for Solving Subproblems

Solve Smallest subproblem first

\[{\color{magenta}Cut(3)} = \max \begin{cases} {\color{magenta}Cut(2)} + \color{blue}{P[1]} \\ {\color{magenta}Cut(1)} + \color{blue}{P[2]} \\ {\color{magenta}Cut(0)} + \color{blue}{P[3]} \\ \end{cases}\]

Cut(i):	0
Length:	0	1	2	3	4	5	6	7	8	9	10

3. Select a Good Order for Solving Subproblems

Solve Smallest subproblem first

\[{\color{magenta}Cut(4)} = \max \begin{cases} {\color{magenta}Cut(3)} + \color{blue}{P[1]} \\ {\color{magenta}Cut(2)} + \color{blue}{P[2]} \\ {\color{magenta}Cut(1)} + \color{blue}{P[3]} \\ {\color{magenta}Cut(0)} + \color{blue}{P[4]} \\ \end{cases}\]

Cut(i):	0
Length:	0	1	2	3	4	5	6	7	8	9	10

Log Cutting Pseudocode

Initialize Memory profit
Cut(n):
- profit[0] = 0
- for i=1 to n: // log size
  - best = 0
  - for j = 1 to i: // last cut
    - best = max(best, profit[i-j] + P[j])
  - profit[i] = best
- return profit[n]

Run time: \(O(n^2)\)

How to find the cuts?

This procedure told us the profit, but not the cuts themselves
Idea: remember the choice that you made, then backtrack

Remember the choice made

Initialize Memory profit, choices
Cut(n):
- profit[0] = 0
- for i=1 to n: // log size
  - best = 0
  - for j = 1 to i: // last cut
    - if best < profit[i-j] + P[j]:
      - best = profit[i-j] + P[j]
      - choices[i] = j // gives the size of the last cut
    - profit[i] = best
- return profit[n]

Reconstruct the Cuts

Backtrack through the choices

Choices:	0	1	1	2	4	3	4	1	2	4	3
Length:	0	1	2	3	4	5	6	7	8	9	10

Example to demo Choices[] only.
Profit of 20 is not optimal!

Backtracking Pseudocode

This is similar to the back link in Dijkstra’s shortest path algorithm

i = n
while i > 0:
- print choices[i]
- i = i - choices[i]

Our Example: Getting Optimal Solution

Prices:	1	5	8	9	10	17	17	20	24	30
Length:	1	2	3	4	5	6	7	8	9	10

i	0	1	2	3	4	5	6	7	8	9	10
profit[i]	0	1	5	8	10	13	17	18	22	25	30
choice[i]	0	1	2	3	2	2	6	1	2	3	10

If \(n\) were 5
- Best score is 13
- Cut at choice[n]=2, then cut at
  choice[n-choice[n]]= choice[5-2]= choice[3]=3
If \(n\) were 7
- Best score is 18
- Cut at 1, then cut at 6

Dynamic Programming

Requires Optimal Substructure
- Solution to larger problem contains the (optimal) solutions to smaller ones
Idea:
1. Identify recursive structure of the problem
  - What is the “last thing” done?
2. Save the solution to each subproblem in memory
3. Select a good order for solving subproblems
  - “Top Down”: Solve each recursively
  - “Bottom Up”: Iteratively solve smallest to largest

Matrix Chaining

Readings in CLRS 4th edition: chapter 14, specifically 14.2

Warm-Up

How many arithmetic operations are required to multiply a \(n \times m\) matrix by a \(m \times p\) matrix?

(don’t overthink this)

	\(m\)
\(n\)

	\(p\)
\(\times\) \(m\)

\(m\) multiplications and \(m-1\) additions per element
\(n \cdot p\) elements to compute
Total cost: \(O(m \cdot n \cdot p)\)

Matrix Chaining

Given a sequence of matrices (\(M_1, M_2, \ldots, M_n\)), what is the most efficient way to multiply them?

	\(c_1\)
\(r_1\)	\(M_1\)

	\(c_2\)
\(\times\) \(r_2\)	\(M_2\)

	\(c_3\)
\(\times\) \(r_3\)	\(M_3\)

	\(c_4\)
\(\times\) \(r_4\)	\(M_4\)

Order Matters!

	\(c_1\)
\(r_1\)	\(M_1\)

\(\times\)

	\(c_2\)
\(r_2\)	\(M_2\)

\(\times\)

	\(c_3\)
\(r_3\)	\(M_3\)

	\(c_2\)
\(r_1\)

Note that \(c_1=r_2\) and \(c_2=r_3\)
\((\)\(M_1\) \(\times\) \(M_2\)\()\) \(\times\) \(M_3\)
- uses \(c_1 \cdot r_1 \cdot c_2\) + \(c_2 \cdot r_1 \cdot c_3\) multiplications

Order Matters!

	\(c_1\)
\(r_1\)	\(M_1\)

\(\times\)

	\(c_2\)
\(r_2\)	\(M_2\)

\(\times\)

	\(c_3\)
\(r_3\)	\(M_3\)

	\(c_3\)
\(r_2\)

Note that \(c_1=r_2\) and \(c_2=r_3\)
\(M_1\) \(\times\) \((\)\(M_2\) \(\times\) \(M_3\)\()\)
- uses \(c_1 \cdot r_1 \cdot c_3\) + \(c_2 \cdot r_2 \cdot c_3\) multiplications

Order Matters!

Note that \(c_1=r_2\) and \(c_2=r_3\)
\((\)\(M_1\) \(\times\) \(M_2\)\()\) \(\times\) \(M_3\)
- uses \(c_1 \cdot r_1 \cdot c_2\) + \(c_2 \cdot r_1 \cdot c_3\) multiplications
- \(10 \cdot 7 \cdot 20 + 20 \cdot 7 \cdot 8 = 2520\)
\(M_1\) \(\times\) \((\)\(M_2\) \(\times\) \(M_3\)\()\)
- uses \(c_1 \cdot r_1 \cdot c_3\) + \(c_2 \cdot r_2 \cdot c_3\) multiplications
- \(10 \cdot 7 \cdot 8 + 20 \cdot 10 \cdot 8 = 2160\)

\(M_1=7 \times 10\)
\(M_2=10 \times 20\)
\(M_3 = 20 \times 8\)

\(c_1=10\)
\(c_2=20\)
\(c_3=8\)
\(r_1=7\)
\(r_2=10\)
\(r_3=20\)

Dynamic Programming

Requires Optimal Substructure
- Solution to larger problem contains the (optimal) solutions to smaller ones
Idea:
1. Identify recursive structure of the problem
  - What is the “last thing” done?
2. Save the solution to each subproblem in memory
3. Select a good order for solving subproblems
  - “Top Down”: Solve each recursively
  - “Bottom Up”: Iteratively solve smallest to largest

1. Identify the Recursive Structure of the Problem

\(Best(1,n)\) = cheapest way to mult together \(M_1\) through \(M_n\)

Let \(k\) be the last multiplication that is made
- \(k\) represents the \(\times\) symbol after matrix \(M_k\)
For \(Best(1,10)\), if \(k=5\), then:
- We first multiply \(M_1\) through \(M_5\) together
- We then multiply \(M_6\) through \(M_10\) together
- Lastly, we multiply those two results together
Formally, for \(Best(i,j)\):
- We multiply \(M_i\) through \(M_k\)
- We multiply \(M_{k+1}\) through \(M_j\)
- We multiply those two results together

1. Identify the Recursive Structure of the Problem

\(Best(1,n)\) = cheapest way to mult together \(M_1\) through \(M_n\)

\[\color{magenta}{Best(1,4)} = \min \begin{cases} \color{magenta}{Best(2,4)} + r_1r_2c_4 \\ \ this formula is hidden \\ \ \\ \end{cases}\]

	\(c_4\)
\(r_2\)

	\(c_1\)
\(r_1\)	\(M_1\)

	\(c_2\)
\(\times\) \(r_2\)	\(M_2\)

	\(c_3\)
\(\times\) \(r_3\)	\(M_3\)

	\(c_4\)
\(\times\) \(r_4\)	\(M_4\)

1. Identify the Recursive Structure of the Problem

\(Best(1,n)\) = cheapest way to mult together \(M_1\) through \(M_n\)

\[Best(1,4) = \min \begin{cases} {\color{green}Best(1,1)}+{\color{magenta}Best(2,4)} + r_1r_2c_4 \\ \ \\ \ \\ \end{cases}\]

	\(c_4\)
\(r_2\)

	\(c_1\)
\(r_1\)	\(M_1\)

	\(c_2\)
\(\times\) \(r_2\)	\(M_2\)

	\(c_3\)
\(\times\) \(r_3\)	\(M_3\)

	\(c_4\)
\(\times\) \(r_4\)	\(M_4\)

1. Identify the Recursive Structure of the Problem

\(Best(1,n)\) = cheapest way to mult together \(M_1\) through \(M_n\)

\[Best(1,4) = \min \begin{cases} {\color{green}Best(1,1)}+{\color{magenta}Best(2,4)} + r_1r_2c_4 \\ {\color{green}Best(1,2)} + {\color{magenta}Best(3,4)} + r_1r_3c_4 \\ \ \\ \end{cases}\]

	\(c_2\)
\(r_1\)

	\(c_4\)
\(r_3\)

	\(c_1\)
\(r_1\)	\(M_1\)

	\(c_2\)
\(\times\) \(r_2\)	\(M_2\)

	\(c_3\)
\(\times\) \(r_3\)	\(M_3\)

	\(c_4\)
\(\times\) \(r_4\)	\(M_4\)

1. Identify the Recursive Structure of the Problem

\(Best(1,n)\) = cheapest way to mult together \(M_1\) through \(M_n\)

\[Best(1,4) = \min \begin{cases} {\color{green}Best(1,1)}+{\color{magenta}Best(2,4)} + r_1r_2c_4 \\ {\color{green}Best(1,2)} + {\color{magenta}Best(3,4)} + r_1r_3c_4 \\ {\color{green}Best(1,3)} + {\color{magenta}Best(4,4)} + r_1r_4c_4 \\ \end{cases}\]

	\(c_3\)
\(r_1\)

	\(c_1\)
\(r_1\)	\(M_1\)

	\(c_2\)
\(\times\) \(r_2\)	\(M_2\)

	\(c_3\)
\(\times\) \(r_3\)	\(M_3\)

	\(c_4\)
\(\times\) \(r_4\)	\(M_4\)

1. Identify the Recursive Structure of the Problem

In general:

\(Best(i,j)\) = cheapest way to multiply together \(M_i\) through \(M_j\)

\(Best(i,j) = \min_{k=i}^{j-1} \left( {\color{green}Best(i,k)} + {\color{magenta}Best(k+1,j)}+r_ir_{k+1}c_j \right)\)

\(Best(i,i)=0\)

\(Best(1,n) = \min \begin{cases} {\color{green}Best(1,1)} + {\color{magenta}Best(2,n)} + r_1r_2c_n \\ {\color{green}Best(1,2)} + {\color{magenta}Best(3,n)} + r_1r_3c_n \\ {\color{green}Best(1,3)} + {\color{magenta}Best(4,n)} + r_1r_4c_n \\ {\color{green}Best(1,4)} + {\color{magenta}Best(5,n)} + r_1r_5c_n \\ \ldots \\ {\color{green}Best(1,n-1)} + {\color{magenta}Best(n,n)} + r_1r_nc_n \\ \end{cases}\)

Dynamic Programming

Requires Optimal Substructure
- Solution to larger problem contains the (optimal) solutions to smaller ones
Idea:
1. Identify recursive structure of the problem
  - What is the “last thing” done?
2. Save the solution to each subproblem in memory
3. Select a good order for solving subproblems
  - “Top Down”: Solve each recursively
  - “Bottom Up”: Iteratively solve smallest to largest

2. Save Subsolutions in Memory

In general:

\(Best(i,j)\) = cheapest way to multiply together \(M_i\) through \(M_j\)

If \(Best(i,j)\) is in memory, read it and done

\(Best(i,j) = \min_{k=i}^{j-1} \left( {\color{green}Best(i,k)} + {\color{magenta}Best(k+1,j)}+r_ir_{k+1}c_j \right)\)

Read \(\color{green}{Best(i,k)}\) and/or \(\color{magenta}{Best(k+1,j)}\) from memory, if available
Save computed \(Best(i,j)\) to memory

\(Best(i,i)=0\)

Dynamic Programming

Requires Optimal Substructure
- Solution to larger problem contains the (optimal) solutions to smaller ones
Idea:
1. Identify recursive structure of the problem
  - What is the “last thing” done?
2. Save the solution to each subproblem in memory
3. Select a good order for solving subproblems
  - “Top Down”: Solve each recursively
  - “Bottom Up”: Iteratively solve smallest to largest

3. Select a good order for solving subproblems

In general:

\(Best(i,j)\) = cheapest way to multiply together \(M_i\) through \(M_j\)

If \(Best(i,j)\) is in memory, read it and done

\(Best(i,j) = \min_{k=i}^{j-1} \left( \color{green}{Best(i,k)} + \color{magenta}{Best(k+1,j)}+r_ir_{k+1}c_j \right)\)

Read \(\color{green}{Best(i,k)}\) and/or \(\color{magenta}{Best(k+1,j)}\) from memory, if available
Save computed \(Best(i,j)\) to memory

\(Best(i,i)=0\)

3. Select a good order for solving subproblems

	\(35\)
\(30\)	\(M_1\)

\(\times\)

	\(15\)
\(35\)	\(M_2\)

\(\times\)

	\(5\)
\(15\)	\(M_3\)

\(\times\)

	\(10\)
\(5\)	\(M_4\)

\(\times\)

	\(20\)
\(10\)	\(M_5\)

\(\times\)

	\(25\)
\(20\)	\(M_6\)

\(\scriptsize Best(i,j) = \min_{k=i}^{j-1} \left( {\color{green}Best(i,k)} + {\color{magenta}Best(k+1,j)}+r_ir_{k+1}c_j \right)\)
\(\scriptsize Best(i,i)=0\)

\(j=\)	\(1\)	\(2\)	\(3\)	\(4\)	\(5\)	\(6\)
	0						1
		0					2
			0				3	\(=i\)
				0			4
					0		5
						0	6

3. Select a good order for solving subproblems

	\(35\)
\(30\)	\(M_1\)

\(\times\)

	\(15\)
\(35\)	\(M_2\)

\(\times\)

	\(5\)
\(15\)	\(M_3\)

\(\times\)

	\(10\)
\(5\)	\(M_4\)

\(\times\)

	\(20\)
\(10\)	\(M_5\)

\(\times\)

	\(25\)
\(20\)	\(M_6\)

\(\scriptsize Best(i,j) = \min_{k=i}^{j-1} \left( {\color{green}Best(i,k)} + {\color{magenta}Best(k+1,j)}+r_ir_{k+1}c_j \right)\)
\(\scriptsize Best(i,i)=0\)

\(\small Best(1,2) = \min\)

\(\small \begin{cases} \ \\ \ \\ {\color{green}Best(1,1)} + {\color{magenta}Best(2,2)} + r_1r_2c_2 \\ \ \\ \ \\ \end{cases}\)

\(j=\)	\(1\)	\(2\)	\(3\)	\(4\)	\(5\)	\(6\)
	0	15750					1
		0					2
			0				3	\(=i\)
				0			4
					0		5
						0	6

3. Select a good order for solving subproblems

	\(35\)
\(30\)	\(M_1\)

\(\times\)

	\(15\)
\(35\)	\(M_2\)

\(\times\)

	\(5\)
\(15\)	\(M_3\)

\(\times\)

	\(10\)
\(5\)	\(M_4\)

\(\times\)

	\(20\)
\(10\)	\(M_5\)

\(\times\)

	\(25\)
\(20\)	\(M_6\)

\(\scriptsize Best(i,j) = \min_{k=i}^{j-1} \left( {\color{green}Best(i,k)} + {\color{magenta}Best(k+1,j)}+r_ir_{k+1}c_j \right)\)
\(\scriptsize Best(i,i)=0\)

\(\small Best(2,3) = \min\)

\(\small \begin{cases} \ \\ \ \\ {\color{green}Best(2,2)} + {\color{magenta}Best(3,3)} + r_2r_3c_3 \\ \ \\ \ \\ \end{cases}\)

\(j=\)	\(1\)	\(2\)	\(3\)	\(4\)	\(5\)	\(6\)
	0	15750					1
		0	2625				2
			0				3	\(=i\)
				0			4
					0		5
						0	6

3. Select a good order for solving subproblems

	\(35\)
\(30\)	\(M_1\)

\(\times\)

	\(15\)
\(35\)	\(M_2\)

\(\times\)

	\(5\)
\(15\)	\(M_3\)

\(\times\)

	\(10\)
\(5\)	\(M_4\)

\(\times\)

	\(20\)
\(10\)	\(M_5\)

\(\times\)

	\(25\)
\(20\)	\(M_6\)

\(\scriptsize Best(i,j) = \min_{k=i}^{j-1} \left( {\color{green}Best(i,k)} + {\color{magenta}Best(k+1,j)}+r_ir_{k+1}c_j \right)\)
\(\scriptsize Best(i,i)=0\)

\(j=\)	\(1\)	\(2\)	\(3\)	\(4\)	\(5\)	\(6\)
	0	15750					1
		0	2625				2
			0	750			3	\(=i\)
				0	1000		4
					0	5000	5
						0	6

3. Select a good order for solving subproblems

	\(35\)
\(30\)	\(M_1\)

\(\times\)

	\(15\)
\(35\)	\(M_2\)

\(\times\)

	\(5\)
\(15\)	\(M_3\)

\(\times\)

	\(10\)
\(5\)	\(M_4\)

\(\times\)

	\(20\)
\(10\)	\(M_5\)

\(\times\)

	\(25\)
\(20\)	\(M_6\)

\(\scriptsize Best(i,j) = \min_{k=i}^{j-1} \left( {\color{green}Best(i,k)} + {\color{magenta}Best(k+1,j)}+r_ir_{k+1}c_j \right)\)
\(\scriptsize Best(i,i)=0\)

\(r_1r_2c_3=30 \cdot 35 \cdot 5=5250\)

\(r_1r_3c_3=30 \cdot 15 \cdot 5=2250\)

\(\small Best(1,3) = \min\)

\(\small \begin{cases} \ (\text{below: }0+2625+5250=7875) \\ {\color{green}Best(1,1)} + {\color{magenta}Best(2,3)} + r_1r_2c_3 \\ {\color{green}Best(1,2)} + {\color{magenta}Best(3,3)} + r_1r_3c_3 \\ \ (\text{above: }15750+0+2250=18000) \\ \ \\ \end{cases}\)

\(\small Best(1,3) = \min\)

\(\small \begin{cases} \ \\ {\color{green}Best(1,1)} + {\color{magenta}Best(2,3)} + r_1r_2c_3 \\ {\color{green}Best(1,2)} + {\color{magenta}Best(3,3)} + r_1r_3c_3 \\ \ \\ \ \\ \end{cases}\)

\(j=\)	\(1\)	\(2\)	\(3\)	\(4\)	\(5\)	\(6\)
	0	15750	7875				1
		0	2625				2
			0	750			3	\(=i\)
				0	1000		4
					0	5000	5
						0	6

3. Select a good order for solving subproblems

	\(35\)
\(30\)	\(M_1\)

\(\times\)

	\(15\)
\(35\)	\(M_2\)

\(\times\)

	\(5\)
\(15\)	\(M_3\)

\(\times\)

	\(10\)
\(5\)	\(M_4\)

\(\times\)

	\(20\)
\(10\)	\(M_5\)

\(\times\)

	\(25\)
\(20\)	\(M_6\)

\(\scriptsize Best(i,j) = \min_{k=i}^{j-1} \left( {\color{green}Best(i,k)} + {\color{magenta}Best(k+1,j)}+r_ir_{k+1}c_j \right)\)
\(\scriptsize Best(i,i)=0\)

To find \(Best(i,j)\): need all preceeding terms of row \(i\) and column \(j\)

(In other words, everything below and to the left)

Conclusion: solve in order of diagonal

\(j=\)	\(1\)	\(2\)	\(3\)	\(4\)	\(5\)	\(6\)
	0	15750	7875				1
		0	2625				2
			0	750			3	\(=i\)
				0	1000		4
					0	5000	5
						0	6

Matrix Chaining

	\(35\)
\(30\)	\(M_1\)

\(\times\)

	\(15\)
\(35\)	\(M_2\)

\(\times\)

	\(5\)
\(15\)	\(M_3\)

\(\times\)

	\(10\)
\(5\)	\(M_4\)

\(\times\)

	\(20\)
\(10\)	\(M_5\)

\(\times\)

	\(25\)
\(20\)	\(M_6\)

\(\scriptsize Best(i,j) = \min_{k=i}^{j-1} \left( {\color{green}Best(i,k)} + {\color{magenta}Best(k+1,j)}+r_ir_{k+1}c_j \right)\)
\(\scriptsize Best(i,i)=0\)

\(\small Best(1,6) = \min\)

\(\small \begin{cases} {\color{green}Best(1,1)} + {\color{magenta}Best(2,6)} + r_1r_2c_6 \\ {\color{green}Best(1,2)} + {\color{magenta}Best(3,6)} + r_1r_3c_6 \\ {\color{green}Best(1,3)} + {\color{magenta}Best(4,6)} + r_1r_4c_6 \\ {\color{green}Best(1,4)} + {\color{magenta}Best(5,6)} + r_1r_5c_6 \\ {\color{green}Best(1,5)} + {\color{magenta}Best(6,6)} + r_1r_6c_6 \\ \end{cases}\)

\(j=\)	\(1\)	\(2\)	\(3\)	\(4\)	\(5\)	\(6\)
	0	15750	7875	9375	11875	15125	1
		0	2625	4375	7125	10500	2
			0	750	2500	5375	3	\(=i\)
				0	1000	3500	4
					0	5000	5
						0	6

Run Time

Initialize \(Best[i,i]\) to be all 0s
Starting at each main diagonal, working to the upper-right, fill in each cell using:

\(\small Best[i,i]=0\)
\(\small \begin{align} Best[i,j] = \min_{k=i}^{j-1} ( & {\color{green}Best(i,k)} + \\ & {\color{magenta}Best(k+1,j)} + \\ & r_ir_{k+1}c_j ) \end{align}\)

\(\Theta(n^2)\) cells in the array

\(\Theta(n)\) options for each cell

(\(n\) is the number of matrices)

Each “call” to \(Best(i,j)\) is an
\(O(1)\) memory lookup

\(\Theta(n^3)\) overall run time

Backtrack to find the best order

“Remember” which choice of \(k\) was the minimum at each cell

\(\scriptsize Best(i,j) = \min_{k=i}^{j-1} \left( {\color{green}Best(i,k)} + {\color{magenta}Best(k+1,j)}+r_ir_{k+1}c_j \right)\)
\(\scriptsize Best(i,i)=0\)

\(\small Best(1,6) = \min\)

\(\small \begin{cases} {\color{green}Best(1,1)} + {\color{magenta}Best(2,6)} + r_1r_2c_6 \\ {\color{green}Best(1,2)} + {\color{magenta}Best(3,6)} + r_1r_3c_6 \\ {\color{red}Best(1,3) + Best(4,6) + r_1r_4c_6} \\ {\color{green}Best(1,4)} + {\color{magenta}Best(5,6)} + r_1r_5c_6 \\ {\color{green}Best(1,5)} + {\color{magenta}Best(6,6)} + r_1r_6c_6 \\ \end{cases}\)

\(j=\)	\(1\)	\(2\)	\(3\)	\(4\)	\(5\)	\(6\)
	0	15750	7875 1	9375	11875	15125 3	1
		0	2625	4375	7125	10500	2
			0	750	2500	5375	3	\(=i\)
				0	1000	3500 5	4
					0	5000	5
						0	6

Matrix Chaining

(

	\(35\)
\(30\)	\(M_1\)

\(\times\)

(

	\(15\)
\(35\)	\(M_2\)

\(\times\)

	\(5\)
\(15\)	\(M_3\)

)

\(\times\)

(

	\(10\)
\(5\)	\(M_4\)

\(\times\)

	\(20\)
\(10\)	\(M_5\)

)

\(\times\)

	\(25\)
\(20\)	\(M_6\)

)

\(\scriptsize Best(i,j) = \min_{k=i}^{j-1} \left( {\color{green}Best(i,k)} + {\color{magenta}Best(k+1,j)}+r_ir_{k+1}c_j \right)\)
\(\scriptsize Best(i,i)=0\)

\(j=\)	\(1\)	\(2\)	\(3\)	\(4\)	\(5\)	\(6\)
	0	15750	7875 1	9375	11875	15125 3	1
		0	2625	4375	7125	10500	2
			0	750	2500	5375	3	\(=i\)
				0	1000	3500 5	4
					0	5000	5
						0	6

Storing and Recovering Optimal Solution

Maintain table choice[i,j] in addition to Best table
- choice[i,j] = k means the best “split” was right after \(M_k\)
- Work backwards from value for whole problem, choice[1,n]
- Note: choice[i,i+1] = i because there are just 2 matrices
From our example:
- choice[1,6] = 3. So \([M_1 \times M_2 \times M_3] \times [M_4 \times M_5 \times M_6]\)
- We then need choice[1,3] = 1. So \([M_1 \times (M_2 \times M_3)]\)
- Also need choice[4,6] = 5. So \([(M_4 \times M_5) \times M_6]\)
- Overall: \([M_1 \times (M_2 \times M_3)] \times [(M_4 \times M_5) \times M_6]\)

Dynamic Programming

Requires Optimal Substructure
- Solution to larger problem contains the (optimal) solutions to smaller ones
Idea:
1. Identify recursive structure of the problem
  - What is the “last thing” done?
2. Save the solution to each subproblem in memory
3. Select a good order for solving subproblems
  - “Top Down”: Solve each recursively
  - “Bottom Up”: Iteratively solve smallest to largest

Making Change

Readings in CLRS 4th edition: chapter 14

Warm-Up

Remember change making?

Given access to unlimited quantities of pennies, nickels, dimes, toms, and quarters (worth value 1, 5, 10, 11, 25 respectively), give 90 cents change using the fewest number of coins.

11
cents

Remember: Greedy Change Making Algorithm

Given: target value \(x\), list of coins \(C=[c_1, \ldots, c_n]\)
- For the US, \(C=[1,5,10,25]\)
Repeatedly select the largest coin less than the remaining target value

while ( x > 0 )
- let \(c = \max(c_i \in C | c_i \le x)\)
- print \(c\)
- \(x=x-c\)

Observation: We can rewrite this to take \(\lfloor n/c \rfloor\) copies of the next largest coin at each step, and reduce \(x\) by \(c \cdot \lfloor n/c \rfloor\). Also avoid call to max() by choosing next \(c_i\) from largest to smallest (sort \(C\) first).

Greedy Solution

90 cents

11
cents

Correct Solution

90 cents

Why does greedy always work for US coins?

If \(x<5\), then pennies only
- Else 5 pennies can be exchanged for a nickel
- Only case where Greedy uses pennies
If \(x \le 5 < 10\), we must have a nickel
- Else 2 nickels can be exchanged for a dime
- Only case where Greedy uses nickels
If \(10 \le x < 25\), we must have at least 1 dime
- Else 3 dimes can be exchanged for a quarter and a nickel
- Only case where Greedy uses dimes
If \(x \ge 25\), we must have at least 1 quarter
- Only case where Greedy uses quarters

Dynamic Programming

Requires Optimal Substructure
- Solution to larger problem contains the (optimal) solutions to smaller ones
Idea:
1. Identify recursive structure of the problem
  - What is the “last thing” done?
2. Save the solution to each subproblem in memory
3. Select a good order for solving subproblems
  - “Top Down”: Solve each recursively
  - “Bottom Up”: Iteratively solve smallest to largest

1. Identify the Recursive Structure of the Problem

\(Change(n)\): minimum number of coins needed to give change for \(n\) cents

Possibilities for last coin	Coins needed	When to do
	\(Change(n-25)+1\)	if \(n \ge 25\)
	\(Change(n-11)+1\)	if \(n \ge 11\)
	\(Change(n-10)+1\)	if \(n \ge 10\)
	\(Change(n-5)+1\)	if \(n \ge 5\)
	\(Change(n-1)+1\)	if \(n \ge 1\)

1. Identify the Recursive Structure of the Problem

\(Change(n)\): minimum number of coins needed to give change for cents

\[Change(n) = \min \begin{cases} Change(n-25)+1 \text{ if } n \ge 25 \\ Change(n-11)+1 \text{ if } n \ge 11 \\ Change(n-10)+1 \text{ if } n \ge 10 \\ Change(n-5)+1 \text{ if } n \ge 5 \\ Change(n-1)+1 \text{ if } n \ge 1 \\ \end{cases}\]

Correctness: The optimal solution must be contained in one of these configurations

Base Case: \(Change(0)=0\)

Running time: \(O(k \cdot n)\)

Is this efficient?

Input size is \(O(k \log n)\)

\(k\) is the number of coins

No, this is pseudo-polynomial time

Seam Carving

Readings in CLRS 4th edition: chapter 14

Seam Carving

Method for image resizing that doesn’t scale/crop the image

Cropping

Removes a “block” of pixels

→

Scaling

Removes “stripes” of pixels

→

(There are more visually pleasing ways to scale images)

Seam Carving

Removes “least energy seam” of pixels

https://trekhleb.dev/js-image-carver/

→

Seam Carving

Method for image resizing that doesn’t scale/crop the image

Cropped	Scaled	Carved

Seattle Skyline

Energy of a Seam

Sum of the energies of each pixel
- \(e(p)=\) energy of pixel \(p\)

Many choices for pixel energy
- Change of gradient (how much the color of this pixel differs from its neighbors)
- Shortest path (more color change means more distance)
- Particular choice doesn’t matter, we use it as a “black box”

Restriction: seam pixels go up or diagonally up, not to the side
Goal: find least-energy seam to remove

Dynamic Programming

Requires Optimal Substructure
- Solution to larger problem contains the (optimal) solutions to smaller ones
Idea:
1. Identify recursive structure of the problem
  - What is the “last thing” done?
2. Save the solution to each subproblem in memory
3. Select a good order for solving subproblems
  - “Top Down”: Solve each recursively
  - “Bottom Up”: Iteratively solve smallest to largest

1. Identify the Recursive Structure of the Problem

Let \({\color{red}S(i,j)}=\) least energy seam from the bottom of the image up to pixel \(p_{i,j}\)

\(p_{i,j}\)

Computing \(\color{pink}S(n,k)\)

Assume we know the least energy seams for all of row \(n-1\) (i.e., we know \(S(n-1,\ell)\) for all \(\ell\))

Known
through
\(n-1\)

\(p_{n,k}\)

\(m\)

Computing \(\color{pink}S(n,k)\)

Assume we know the least energy seams for all of row \(n-1\) (i.e., we know \(S(n-1,\ell)\) for all \(\ell\))

\(p_{n,k}\)

\(\color{white}S(n,k)\)

\(\color{white}S(n-1,k-1)\)

\(\color{white}S(n-1,k)\)

\(\color{white}S(n-1,k+1)\)

\[{\color{red}S(n,k)} = \min \begin{cases} {\color{blue}S(n-1,k-1)} & + e(p_{n,k}) \\ {\color{purple}S(n-1,k)} & + e(p_{n,k}) \\ {\color{magenta}S(n-1,k+1)} & + e(p_{n,k}) \\ \end{cases}\]

Finding the Least Energy Seam

Want to delete the least energy seam going from bottom to top, so delete: \(\min_{k=1}^m({\color{red}S(n,k)})\)

\(n\)

\(p_{n,k}\)

\(m\)

Dynamic Programming

Requires Optimal Substructure
- Solution to larger problem contains the (optimal) solutions to smaller ones
Idea:
1. Identify recursive structure of the problem
  - What is the “last thing” done?
2. Save the solution to each subproblem in memory
3. Select a good order for solving subproblems
  - “Top Down”: Solve each recursively
  - “Bottom Up”: Iteratively solve smallest to largest

Computing \(\color{pink}S(n,k)\)

Assume we know the least energy seams for all of row \(n-1\) (i.e., we know \(S(n-1,\ell)\) for all \(\ell\))

\(p_{n,k}\)

\(\color{white}S(n,k)\)

\(\color{white}S(n-1,k-1)\)

\(\color{white}S(n-1,k)\)

\(\color{white}S(n-1,k+1)\)

\[{\color{red}S(n,k)} = \min \begin{cases} {\color{blue}S(n-1,k-1)} & + e(p_{n,k}) \\ {\color{purple}S(n-1,k)} & + e(p_{n,k}) \\ {\color{magenta}S(n-1,k+1)} & + e(p_{n,k}) \\ \end{cases}\]

Finding the Least Energy Seam

Want to delete the least energy seam going from bottom to top, so delete: \(\min_{k=1}^m({\color{red}S(n,k)})\)

\(n\)

\(p_{n,k}\)

\(m\)

Dynamic Programming

Requires Optimal Substructure
- Solution to larger problem contains the (optimal) solutions to smaller ones
Idea:
1. Identify recursive structure of the problem
  - What is the “last thing” done?
2. Save the solution to each subproblem in memory
3. Select a good order for solving subproblems
  - “Top Down”: Solve each recursively
  - “Bottom Up”: Iteratively solve smallest to largest

Bring It All Together

Start from bottom of image (row 1), solve up to top
Initialize \(S(1,k)=e(p_{1,k})\) for each pixel in row 1	\(\color{green}\Theta(m)\)
	\(\color{red}\Theta(n \cdot m)\)
	\(\Theta(n+m)\)
	Energy of the seam initialized to the energy of that pixel

Bring It All Together

Start from bottom of image (row 1), solve up to top
Initialize \(S(1,k)=e(p_{1,k})\) for each pixel \(p_{1,k}\)	\(\color{green}\Theta(m)\)
For \(i \ge 2\) find \({\color{red}S(i,k)} = \min \begin{cases} {\color{purple}S(i-1,k-1)} & + e(p_{i,k}) \\ {\color{blue}S(i-1,k)} & + e(p_{i,k}) \\ {\color{magenta}S(i-1,k+1)} & + e(p_{i,k}) \\ \end{cases}\)	\(\color{red}\Theta(n \cdot m)\)
	\(\Theta(n+m)\)
	Energy of the seam initialized to the energy of that pixel

Finding the Seam

Start from bottom of image (row 1), solve up to top
Initialize \(S(1,k)=e(p_{1,k})\) for each pixel \(p_{1,k}\)	\(\color{green}\Theta(m)\)
For \(i \ge 2\) find \({\color{red}S(i,k)} = \min \begin{cases} {\color{purple}S(i-1,k-1)} & + e(p_{i,k}) \\ {\color{blue}S(i-1,k)} & + e(p_{i,k}) \\ {\color{magenta}S(i-1,k+1)} & + e(p_{i,k}) \\ \end{cases}\)	\(\color{red}\Theta(n \cdot m)\)
Pick min \(\color{red}S(n,k)\) from top row, backtrack, deleting pixels	\(\Theta(n+m)\)
	Energy of the seam initialized to the energy of that pixel

Run Time?

Start from bottom of image (row 1), solve up to top
Initialize \(S(1,k)=e(p_{1,k})\) for each pixel \(p_{1,k}\)	\(\color{green}\Theta(m)\)
For \(i \ge 2\) find \({\color{red}S(i,k)} = \min \begin{cases} {\color{purple}S(i-1,k-1)} & + e(p_{i,k}) \\ {\color{blue}S(i-1,k)} & + e(p_{i,k}) \\ {\color{magenta}S(i-1,k+1)} & + e(p_{i,k}) \\ \end{cases}\)	\(\color{red}\Theta(n \cdot m)\)
Pick min \(\color{red}S(n,k)\) from top row, backtrack, deleting pixels	\(\Theta(n+m)\)
	Energy of the seam initialized to the energy of that pixel

Repeated Seam Removal

Only need to update pixels dependant on the removed seam

\(2n\) pixels change	\(\Theta(2n)\) time to update pixels
	\(\Theta(n+m)\) to find min+backtrack

Longest Common Subsequence

Readings in CLRS 4th edition: chapter 14, specifically 14.4

Longest Common Subsequence

Given two sequences \(X\) and \(Y\), find the length of their longest common subsequence

Example:
𝑋 = 𝐴𝑇𝐶𝑇𝐺𝐴𝑇
𝑌 = 𝑇𝐺𝐶𝐴𝑇𝐴
𝐿𝐶𝑆 = 𝑇𝐶𝑇𝐴

Brute force: compare every subsequence of \(X\) with \(Y\): \(\Omega(2^n)\)

Dynamic Programming

Requires Optimal Substructure
- Solution to larger problem contains the (optimal) solutions to smaller ones
Idea:
1. Identify recursive structure of the problem
  - What is the “last thing” done?
2. Save the solution to each subproblem in memory
3. Select a good order for solving subproblems
  - “Top Down”: Solve each recursively
  - “Bottom Up”: Iteratively solve smallest to largest

1. Identify the Recursive Structure of the Problem

Let \(LCS(i.j)=\) length of the LCS for the first \(i\) characters of \(X\), first \(j\) characters of \(Y\)

Find \(\color{magenta}LCS(i,j)\):

Case 1: \(\color{magenta}X[i]=Y[j]\)	X = ATCTGCGT Y = TGCATAT
	\(LCS(i,j)=LCS(i-1,j-1)+1\)
Case 2: \(\color{magenta}X[i]\ne Y[j]\)
X = ATCTGCGA Y = TGCATAT	X = ATCTGCGT Y = TGCATAC
\(LCS(i,j)=LCS(i,j-1)\)	\(LCS(i,j)=LCS(i-1,j)\)

\[LCS(i,j) = \begin{cases} 0 & \text{if } i=0 \text{ or } j=0 \\ {\color{green}LCS(i-1,j-1)+1} & \text{if } X[i]=Y[j] \\ {\color{blue}\max(LCS(i,j-1),LCS(i-1,j))} & \text{otherwise} \\ \end{cases}\]

Dynamic Programming

Requires Optimal Substructure
- Solution to larger problem contains the (optimal) solutions to smaller ones
Idea:
1. Identify recursive structure of the problem
  - What is the “last thing” done?
2. Save the solution to each subproblem in memory
3. Select a good order for solving subproblems
  - “Top Down”: Solve each recursively
  - “Bottom Up”: Iteratively solve smallest to largest

Top-Down Solution with Memoization

We need two functions; one will be recursive

LCS-Length(X, Y): // Y is M’s cols.
- n = length(X)
- m = length(Y)
- Create table M[n,m]
- Assign -1 to all cells M[i,j]
- // get value for entire sequences
- return LCS-recur(X, Y, M, n, m)

0
\(\color{green}LCS(i-1,j-1)+1\)
\(\color{blue}\max(LCS(i,j-1),LCS(i-1,j))\)

if \(i=0\) or \(j=0\)
if \(X[i]=Y[j]\)
otherwise

LCS-recur(X, Y, M, i, j):
- if (i == 0 || j == 0) return 0
- // have we already calculated
- // this subproblem?
- if ( M[i,j] != -1 ) return M[i,j]
- if ( X[i] == Y[j] )
  - M[i,j] = LCS-recur(X, Y, M, i-1, j-1) + 1
- else // X[i] != Y[j]
  - M[i,j] = max( LCS-recur(X, Y, M, i-1, j),
    - LCS-recur(X, Y, M, i, j-1) )
- return M[i,j]

Dynamic Programming

Requires Optimal Substructure
- Solution to larger problem contains the (optimal) solutions to smaller ones
Idea:
1. Identify recursive structure of the problem
  - What is the “last thing” done?
2. Save the solution to each subproblem in memory
3. Select a good order for solving subproblems
  - “Top Down”: Solve each recursively
  - “Bottom Up”: Iteratively solve smallest to largest

Solve in a Good Order

\[\scriptstyle LCS(i,j) = \begin{cases} 0 & \text{if } i=0 \text{ or } j=0 \\ {\color{green}LCS(i-1,j-1)+1} & \text{if } X[i]=Y[j] \\ {\color{blue}\max(LCS(i,j-1),LCS(i-1,j))} & \text{otherwise} \\ \end{cases}\]

To fill in cell \((i,j)\) we need cells \((i-1,j-1)\), \((i-1,j)\), and \((i,j-1)\) Fill from top → bottom, left → right (with any preference)

LCS Length Algorithm: Bottom-Up

LCS-Length(X, Y) // Y for M’s rows, X for its columns
- n = length(X) // get the length of X
- m = length(Y) // get the length of Y
- for i = 1 to n: M[i,0] = 0 // special case: X0
- for j = 1 to m: M[0,j] = 0 // special case: Y0
- for i = 1 to n: // for all Xi
  - for j = 1 to m: // for all Yj
    - if ( X[i] == Y[j] )
      - M[i,j] = M[i-1,j-1] + 1
    - else
      - M[i,j] = max( M[i-1,j], M[i,j-1] )
- return M[n,m] // return LCS length for Y and X

Run Time?

Run time: \(\Theta(n \cdot m)\) (for \(|X|=n\), \(|Y|=m\))

Reconstructing the LCS example 1

Start from bottom right,
if symbols matched, print that symbol then go diagonally,
else go to largest adjacent

Reconstructing the LCS example 2

Start from bottom right,
if symbols matched, print that symbol then go diagonally,
else go to largest adjacent

Reconstructing the LCS example 3

Start from bottom right,
if symbols matched, print that symbol then go diagonally,
else go to largest adjacent

Gerrymandering

Readings in CLRS 4th edition: chapter 14

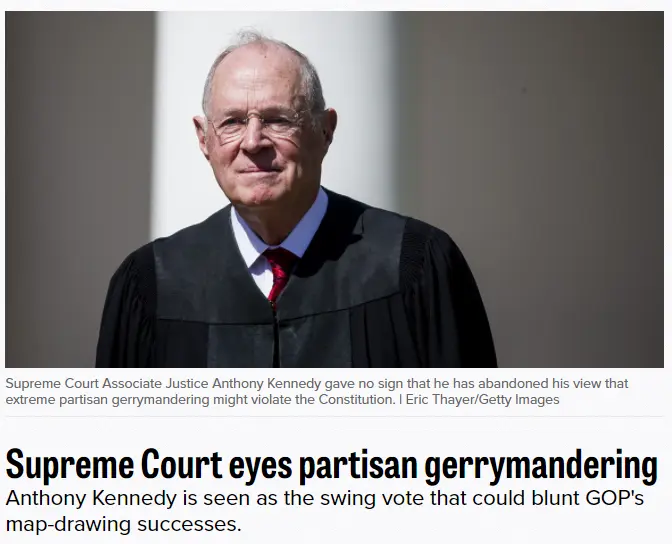
Gerrymandering

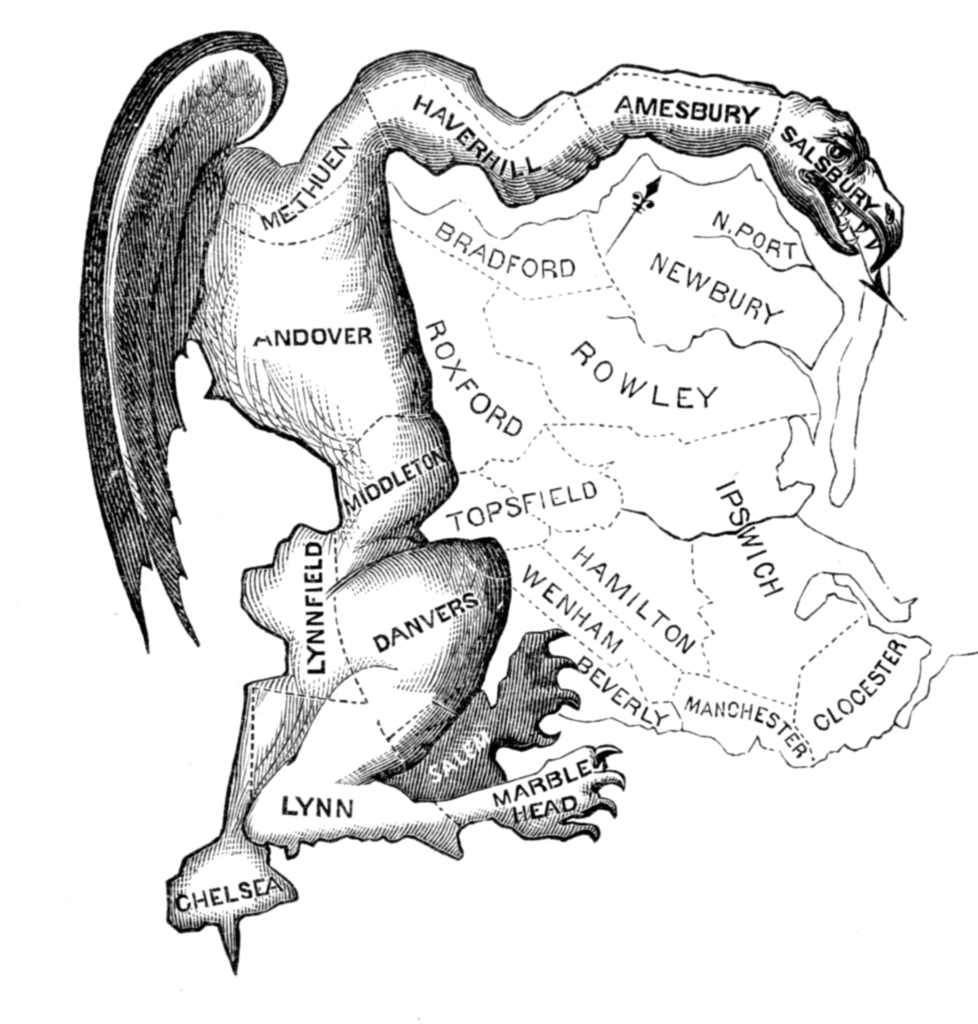
Manipulating electoral district boundaries to favor one political party over others
Coined in an 1812 Political cartoon
Governor Elbridge Gerry signed a bill that redistricted Massachusetts to benefit his Democratic-Republican Party

According to the Supreme Court

Gerrymandering cannot be used to:
- Disadvantage racial/ethnic/religious groups
It can be used to:
- Disadvantage political parties

Virginia’s 5th District (until 2023)

Virginia’s 5th District in 2018

	Votes	Percent
	165,339	53.3%
	145,040	46.7%

End of VA gerrymandering

A 2020 state constitutional amendment changed how the state sets districts
- Wikipedia article
The redistricting committee:
- Four state senators, two from each party
- Four state house delegate members, two from each party
- Eight citizens
It’s voted on, but not changeable by, the general assembly
- The governor is not involved at all
It passed with 65.69% of the vote

Virginia’s 5th District (today)

Virginia’s congressional districts (today)

Gerrymandering Today

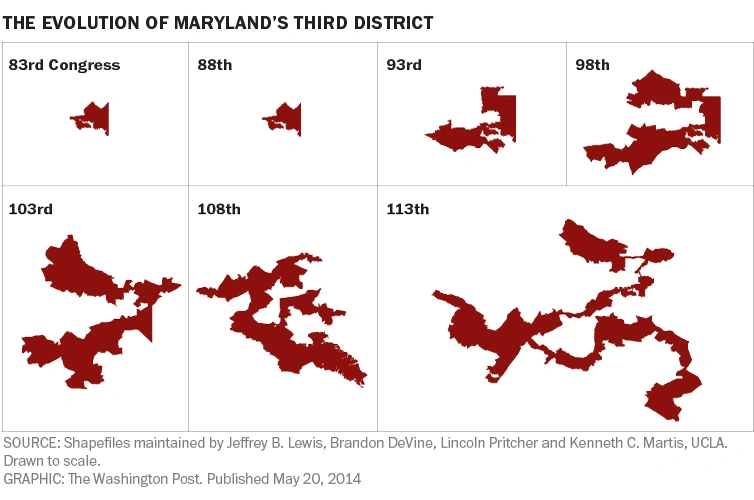
Pennsylvania 2018 controversy

Math and CS professors have been asked to testify in court as to the difficulty in creating some of these districts

https://www.usnews.com/news/national-news/articles/2018-02-20/what-
pennsylvanias-new-court-drawn-congressional-redistricting-looks-like

https://www.heinz.cmu.edu/media/2018/
October/wes-pegden-gerrymandering

“Wesley Pegden, professor of mathematical sciences at Carnegie Mellon University, proved that Pennsylvania’s congressional map was a partisan gerrymander—in fact, he showed that if you made trillions of districtings by making small random perturbations to the map, 99.9999999% of them of them would be fairer than the existing map, a property which is mathematically impossible to be typical for a Congressional districting, regardless of the political geography of a state. His expert testimony during a lawsuit led to the Pennsylvania supreme court throwing out the old map.” https://www.heinz.cmu.edu/media/2018/October/wes-pegden-gerrymandering

How does it work?

States are broken into precincts
All precincts have the same size
We know voting preferences of each precinct
Group precincts into districts to maximize the number of districts won by my party
Consider the district to the right; 5 different ways to split up the voters
- Upper left: 0 yellow, 5 blue
- Upper right: 3 yellow, 2 blue
- Both lower: 2 yellow, 3 blue

How does it work?

States are broken into precincts
All precincts have the same size
We know voting preferences of each precinct
Group precincts into districts to maximize the number of districts won by my party

Overall:
A: 217, B: 183
A: 65 B: 35	A: 45 B: 55
A: 60 B: 40	A: 47 B: 53

\(D_1\)	\(D_2\)
A: 125	A: 92
A: 65 B: 35	A: 45 B: 55
A: 60 B: 40	A: 47 B: 53

\(D_1\)	\(D_2\)
A: 112	A: 105
A: 65 B: 35	A: 45 B: 55
A: 47 B: 53	A: 60 B: 40

Gerrymandering problem statement

Given:
- A list of \(n\) precincts: \(p_1,p_2,\ldots,p_n\)
- Each containing \(m\) voters
- Total of \(m \cdot n\) voters
Output:
- Districts \({\color{magenta}D_1}, {\color{green}D_2} \subset \{ p_1,p_2,\ldots,p_{n} \}\)
- Where \(|{\color{magenta}D_1}| = |{\color{green}D_2}|\)
- \(S({\color{magenta}D_1})>\frac{m \cdot n}{4}\) and \(S({\color{green}D_2})>\frac{m \cdot n}{4}\)
  - \(S(D_i)\) is the number (size) of voters of your party in \(D_i\)
  - \(S(D_i)>\frac{m \cdot n}{4}\) means \(D_i\) is majority your party
- “Failure” if no possible solution

Valid Gerrymandering!

\(\frac{m \cdot n}{4}=m \cdot \frac{n}{2} \cdot \frac{1}{2}\)

\(\color{magenta}D_1\)	\(\color{forestgreen}D_2\)
\(\frac{m \cdot n}{4}\)	\(\frac{m \cdot n}{4}\)
\(\frac{m \cdot n}{4}\)	\(\frac{m \cdot n}{4}\)

Dynamic Programming

Requires Optimal Substructure
- Solution to larger problem contains the (optimal) solutions to smaller ones
Idea:
1. Identify recursive structure of the problem
  - What is the “last thing” done?
2. Save the solution to each subproblem in memory
3. Select a good order for solving subproblems
  - “Top Down”: Solve each recursively
  - “Bottom Up”: Iteratively solve smallest to largest

Consider the last precinct

After assigning first
\(n-1\) precincts
\(p_1,p_2,\ldots,p_{n-1}\)

\(D_1\)
\(k\) precincts
\(x\) voters for \(R\)

\(D_2\)
\(n-k-1\)
precincts
\(y\) voters for \(R\)

If we
assign
\(p_n \text{ to } D_1\)

\(p_n\)

If we
assign
\(p_n \text{ to } D_2\)

\(D_1\)
\(k+1\) precincts
\(x+S(p_n)\) voters for \(R\)

Valid gerrymandering
if: \(k+1=\frac{n}{2}\) (or \(\frac{n}{2}+1\)), \(x+S(p_n), y > \frac{mn}{4}\)

\(D_2\)
\(n-k\) precincts
\(y+S(p_n)\) voters for \(R\)

Valid gerrymandering
if: \(n-k=\frac{n}{2}\) (or \(\frac{n}{2}+1\)), \(x,y+S(p_n) > \frac{mn}{4}\)

\(D_1\)
\(k+1\) precincts
\(x+S(p_n)\) voters for \(R\)

\(D_2\)
\(n-k-1\) precincts
\(y\) voters for \(R\)

Valid gerrymandering if: \(k+1=\frac{n}{2}\) (or \(\frac{n}{2}+1\)),
\(x+S(p_n), y > \frac{mn}{4}\)

World One

\(D_1\)
\(k\) precincts
\(x\) voters for \(R\)

\(D_2\)
\(n-k\) precincts
\(y+S(p_n)\) voters for \(R\)

Valid gerrymandering if: \(n-k=\frac{n}{2}\) (or \(\frac{n}{2}+1\)),
\(x,y+S(p_n) > \frac{mn}{4}\)

World Two

Define Recursive Structure

\(S(j,k,x,y) = \text{True}\)

if from among the first \(j\) precincts:
\(k\) are assigned to \(\color{magenta}D_1\)
exactly \(x\) vote for R in \(\color{magenta}D_1\)
exactly \(y\) vote for R in \(\color{green}D_2\)

\(\color{red}n \times n \times mn \times mn\)

4D Dynamic programming!

True here means that this is a valid state of the world, not a valid gerrymander!

Two ways to satisfy \(S(j,k,x,y)\)

\(D_1\)
\(k-1\) precincts
\(x-S(P_j)\) voters for \(R\)

\(D_2\)
\(j-k\) precincts
\(y\) voters for \(R\)

\(D_1\)
\(k\) precincts
\(x\) voters for \(R\)

\(D_2\)
\(j-k-1\) precincts
\(y-S(p_j)\) voters for \(R\)

\(p_j\)

Then assign
\(p_j\) to \(D_1\)

\(p_j\)

Then assign
\(p_j\) to \(D_2\)

\(S(j,k,x,y)\) true if:
    from among the first \(j\) precincts
    \(k\) are assigned to \(\color{magenta}D_1\)
    exactly \(x\) vote for \(R\) in \(\color{magenta}D_1\)
    exactly \(y\) vote for \(R\) in \(\color{green}D_2\)

\(D_1\)
\(k\) precincts
\(x\) voters for \(R\)

\(D_2\)
\(j-k\) precincts
\(y\) voters for \(R\)

\[S(j,k,x,y) = {\color{magenta}S(j-1,k-1,x-S(p_j),y)} \vee {\color{green}S(j-1,k,x,y-S(p_j))}\]

Final Algorithm

\[\small S(j,k,x,y) = {\color{magenta}S(j-1,k-1,x-S(p_j),y)} \vee {\color{green}S(j-1,k,x,y-S(p_j))}\]

Initialize \(S(0,0,0,0) = \text{True}\)
for \(j=1,\ldots,n\):
- for \(k=1,\ldots,\min(j,\frac{n}{2})\):
  - for \(x=1,\ldots,j \cdot m\):
    - for \(y=1,\ldots,j \cdot m\):

\[\begin{align} S(j,k,x,y) = & {\color{magenta}S(j-1,k-1,x-S(p_j),y)} \vee \\ & {\color{green}S(j-1,k,x,y-S(p_j))} \end{align}\]

Search for True entry at \(S \left( n, \frac{n}{2}, >\frac{m \cdot n}{4}, >\frac{m \cdot n}{4} \right)\)

Gerrymander Run Time

\[\small S(j,k,x,y) = {\color{magenta}S(j-1,k-1,x-S(p_j),y)} \vee {\color{green}S(j-1,k,x,y-S(p_j))}\]

Initialize \(S(0,0,0,0) = \text{True}\) for \(j=1,\ldots,n\): for \(k=1,\ldots,\min(j,\frac{n}{2})\): for \(x=1,\ldots,j \cdot m\): for \(y=1,\ldots,j \cdot m\):	\(\color{red}n\) \(\color{red}n/2\) \(\color{red}n \cdot m\) \(\color{red}n \cdot m\)
\[\begin{align} S(j,k,x,y) = & {\color{magenta}S(j-1,k-1,x-S(p_j),y)} \vee \\ & {\color{green}S(j-1,k,x,y-S(p_j))} \end{align}\]
Total run time: \(\Theta(n^4m^2)\)

\(\color{pink}\Theta(n^4m^2)\)

Input: list of precincts (size \(n\)), number of voters (integer \(m\))
Runtime depends on the value of \(m\), not size of \(m\)
- Run time is exponential in size of input
  - Input size is \(n+|m|=n+\log m\)
Note: Gerrymandering is NP-Complete

Gerrymandering Font

source

CS 3100

Data Structures and Algorithms 2

Dynamic Programming

Introduction

Warm Up

Warm Up

How to compute \(Tile(n)\)?

Recursion Tree

Recursion Tree

Computing \(Tile(n)\) with memory

Computing \(Tile(n)\) with memory

Dynamic Programming

Dynamic Programming

Generic Divide and Conquer Solution

Generic Top-Down DP Solution

Generic Top-Down DP Solution

Computing \(Tile(n)\) with memory “Top Down”

Computing \(Tile(n)\) with memory “Bottom Up”

Dynamic Programming

More on Optimal Substructure Property

Log Cutting

Log Cutting

Greedy Algorithm

Greedy Algorithm

Dynamic Programming

1. Identify Recursive Substructure

Dynamic Programming

3. Select a Good Order for Solving Subproblems

3. Select a Good Order for Solving Subproblems

3. Select a Good Order for Solving Subproblems

3. Select a Good Order for Solving Subproblems

3. Select a Good Order for Solving Subproblems

Log Cutting Pseudocode

How to find the cuts?

Remember the choice made

Reconstruct the Cuts

Backtracking Pseudocode

Our Example: Getting Optimal Solution

Dynamic Programming

Matrix Chaining

Warm-Up

Matrix Chaining

Order Matters!

Order Matters!

Order Matters!

Dynamic Programming

1. Identify the Recursive Structure of the Problem

1. Identify the Recursive Structure of the Problem

1. Identify the Recursive Structure of the Problem

1. Identify the Recursive Structure of the Problem

1. Identify the Recursive Structure of the Problem

1. Identify the Recursive Structure of the Problem

Dynamic Programming

2. Save Subsolutions in Memory

Dynamic Programming

3. Select a good order for solving subproblems

3. Select a good order for solving subproblems

3. Select a good order for solving subproblems

3. Select a good order for solving subproblems

3. Select a good order for solving subproblems

3. Select a good order for solving subproblems

3. Select a good order for solving subproblems

Matrix Chaining

Run Time

Backtrack to find the best order

Matrix Chaining

Storing and Recovering Optimal Solution

Dynamic Programming

Making Change

Warm-Up

Remember: Greedy Change Making Algorithm

Greedy Solution

Correct Solution

Why does greedy always work for US coins?

Dynamic Programming

1. Identify the Recursive Structure of the Problem

1. Identify the Recursive Structure of the Problem

Seam Carving

Seam Carving

Cropping