

This is a friendly reminder on the class policy regarding the use of GenAI on programming assignments in this course. While you may use GenAI to do the equivalent of looking up known information on the web / in a manual, you may NOT use GenAI to generate the solution to any part of this programming assignment. The purpose of the assignment is to practice your problem solving and programming implementation skills on your own. If we find that you have copied significant code generated by AI for this programming assignment, this will be considered an honor violation.
You run a home renovation business called the Dwelling Sprucers Association (DSA) that handles hundreds (maybe even thousands) of projects simultaneously across the country in dozens of cities and states. To accomplish these home renovations, you work with hundreds of contractors who you schedule to perform certain tasks for each renovation project (painting, installing appliances, electrical work, etc.). Your company has a big problem though: You have grown to be so large that managing the schedule of which contractors are going to work on each renovation project has become daunting. Can you write a program that figures out which contractors should work on which project and (more importantly) report how many total days it will take to finish every single project?
Each project is a single building (home, commercial, etc.) that exists in a specified city. In addition, each project needs to have one or more work orders completed in order for the renovation to be finished. Each work order is of a specific type (e.g., painting, electrical, etc.).
There are several contractors who each work on exactly one type of work order (they are only painters, only electrical workers, etc.) but are available to work in one or more of the cities. In addition, each contractor can work a set number of jobs in each day (e.g., painters might be able to handle three projects per day while electricians might only be able to handle one).
Given all of this information: What is the minimum number of days it will take to complete all of the projects? For simplicity, assume that work orders can be handled in parallel with no issue (e.g., the electricians will never get in the way of the painters if they are there at the same time).
Take a look at the example input below (in the “Sample Input” section of this page). In this example, there are four projects (Floryan’s Home, Bloomfield’s Home, Rice Hall, and the VA State Capital Building). Two of these projects are in Charlottesville and two of them are in Richmond. They need a varying number and types of work orders completed.
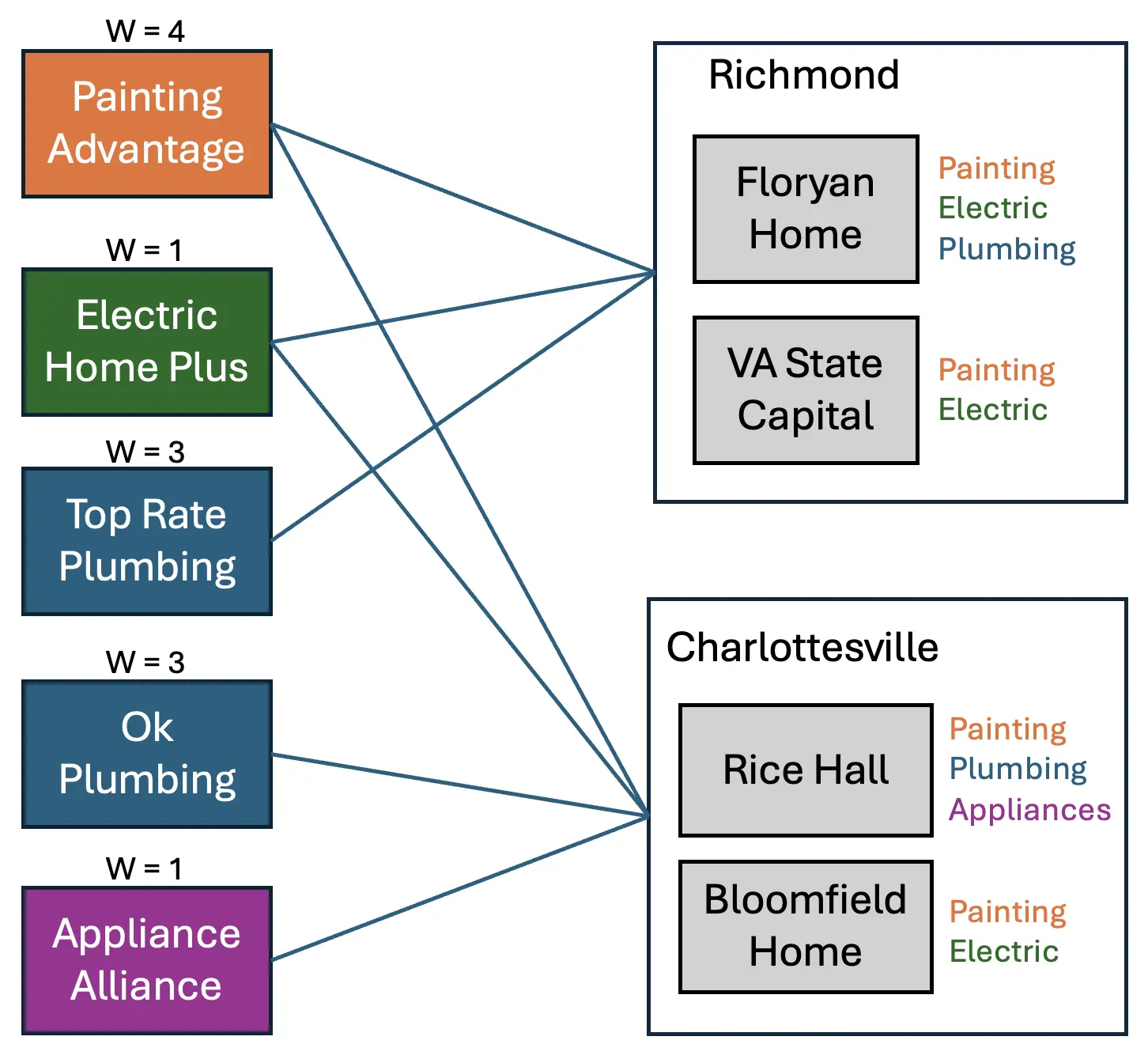
We also have five contractors. One painting company, one electric, two plumbing companies, and one appliance company. Some of the contractors work in both cities and some of them only work in one of the two. The one appliance job can be handled by the appliance company in one day. There are two plumbing jobs but we have two plumbing companies (likely one for each city), so they only need one day as well. The painting company can do four jobs in one day (amazing!) and there are four total paint jobs so that is only one day of work as well. The electrician can only do one job per day and there are three total, so the electrician is the limiting factor, and we will need three days to complete all of the work even though most of it is done after only one day.
The first line of input is 1 ≤ b ≤ 105, the number of buildings that are being renovated. The next b lines will each describe one building. Each line will contain the name of the building (no spaces) followed by the city that building is in following by a list of work orders needed on that building.
After that there will be a number 1 ≤ c ≤ 105, the number of contractors. The rest of the input will contain each contractor’s information one at a time; each contractor’s information is on exactly one line. Each contractor starts with a the name of the contractor (no spaces), followed by 1 ≤ p ≤ 105, the number of places where they are willing to work, following by a number 1 ≤ w ≤ 105, the number of work orders they can complete in one day. The next string on this line will be the one type of work order that company handles (e.g., painting). Following that are p places where the contractor is willing to work. All values on this line are space-separated, and none have spaces in the value (i.e., it is “PaintingAdvantage”, not “Painting Advantage”).
Output the minimum number of days it will take to finish all of the work orders followed by the word “days” (for simplicity, use “days” even if the answer is 1). If it is impossible fulfill all of the work for any reason, output the word “impossible”.
4
FloryanHome Richmond painting electric plumbing
BloomfieldHome Charlottesville painting electric
RiceHall Charlottesville painting plumbing appliances
VAStateCapital Richmond painting electric
5
PaintingAdvantage 2 4 painting Charlottesville Richmond
ElectricHomePlus 2 1 electric Richmond Charlottesville
TopRatePlumbing 1 3 plumbing Richmond
OkPlumbing 1 3 plumbing Charlottesville
ApplianceAlliance 1 1 appliances Charlottesville
3 days
Your solution should involve developing a reduction to network flow, similar to the problems shown in class. You should:
For this assignment, you will need to develop all of your code from scratch on your own.
You are required to reduce this problem to a max-flow problem. You should use the networkx package for Python or the JGraphT package for Java.
The submission system can handle four different programming languages. For each programming language, the name of the submitted file is listed below (you have to have it named that exact name, else it will not compile properly). If you want to program in a different language, email the course email at least three days before it is due (as we have to reconfigure the autograder).
You will submit your completed source code file to Gradescope. There will be a small set of acceptance tests that are NOT COMPREHENSIVE. These acceptance tests are the test cases in the example.in file. It’s up to you to comprehensively test your code. The acceptance tests just verify that you are reading the input correctly and providing the expected output.
Note that when you submit, Gradescope will report your grade as “-/10” or “0/10” – that’s a quirk of Gradescope, and is because the grading tests have not been run (and won’t be run until after all submissions are in). You can look at the results of the individual test cases to see how your program worked